题目内容
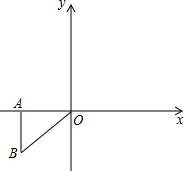 如图,△ABO中,O是坐标原点,A(-
如图,△ABO中,O是坐标原点,A(-| 3 |
| 3 |
(1)①以原点O为位似中心,将△ABO放大,使变换后得到的△CDO与△ABO的位似比为2:1,且D在第一象限内,则C点坐标为(
②将△DOC沿OD折叠,点C落在第一象限的E处,画出图形,并求出点E的坐标;
(2)若抛物线y=ax2+bx(a≠0)过(1)中的E、C两点,求抛物线的解析式;
(3)在(2)中的抛物线EC段(不包括C、E点)上是否存在一点M,使得四边形MEOC面积最大?若存在,求出这个最大值,并求出此时M点的坐标;若不存在,请说明理由.
分析:(1)①首先根据点D的位置确定△COD的位置,然后根据位似比作图,即可得到点C、D的坐标;
②可过E作y轴的垂线,设垂足为F,由于△ODE是由△ODC翻折而得,故OE=OC=2
,∠EOD=∠COD=30°,根据这些条件,即可在Rt△OEF中,通过解直角三角形求出点E的坐标.
(2)在(1)题中,已经求得了E、C的坐标,利用待定系数法求解即可.
(3)四边形MEOC中,△OEC的面积是定值,若四边形的面积最大,则△EMC的面积最大;过M作MN∥y轴,交直线CE于N,设出点M的横坐标,根据抛物线和直线CE的解析式即可得到MN的长,以MN为底,C、E横坐标差的绝对值为高,即可得到△EMC的面积表达式,进而可得到关于四边形MEOC的面积和M点横坐标的函数关系式,根据函数的性质即可得到四边形的面积最大值,及对应的M点坐标.
②可过E作y轴的垂线,设垂足为F,由于△ODE是由△ODC翻折而得,故OE=OC=2
| 3 |
(2)在(1)题中,已经求得了E、C的坐标,利用待定系数法求解即可.
(3)四边形MEOC中,△OEC的面积是定值,若四边形的面积最大,则△EMC的面积最大;过M作MN∥y轴,交直线CE于N,设出点M的横坐标,根据抛物线和直线CE的解析式即可得到MN的长,以MN为底,C、E横坐标差的绝对值为高,即可得到△EMC的面积表达式,进而可得到关于四边形MEOC的面积和M点横坐标的函数关系式,根据函数的性质即可得到四边形的面积最大值,及对应的M点坐标.
解答: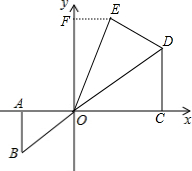 解:(1)①由题意知:OC=2OA=2
解:(1)①由题意知:OC=2OA=2
,
CD=2AB=2;
故C(2
,0),D(2
,2);
②如图,过E作EF⊥y轴于F;
Rt△OCD中,OC=2
,CD=2,则有:
∠DOC=30°;
根据折叠的性质知:
OE=OC=2
,∠EOD=∠DOC=30°;
在Rt△OEF中,OE=2
,∠FOE=30°,
则:FE=
,OF=3,
故E(
,3).
(2)由于抛物线经过E(
,3),C(2
,0),依题意有:
,
解得
,
∴抛物线的解析式为:y=-x2+2
x;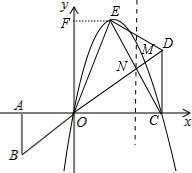
(3)过M作MN∥y轴,交CE于N;
∵E(
,3),C(2
,0),
∴直线EC:y=-
x+6;
设M(x,-x2+2
x),则N(x,-
x+6),
∴MN=-x2+2
x-(-
x+6)=-x2+3
x-6;
∴四边形EMCO的面积S=S△EMC+S△EOC
=
×(-x2+3
x-6)×
+
×2
×3
=-
x2+
x=-
(x-
)2+
;
∴当x=
,即M(
,
)时,四边形OEMC的面积最大,且最大值为
.
 解:(1)①由题意知:OC=2OA=2
解:(1)①由题意知:OC=2OA=2| 3 |
CD=2AB=2;
故C(2
| 3 |
| 3 |
②如图,过E作EF⊥y轴于F;
Rt△OCD中,OC=2
| 3 |
∠DOC=30°;
根据折叠的性质知:
OE=OC=2
| 3 |
在Rt△OEF中,OE=2
| 3 |
则:FE=
| 3 |
故E(
| 3 |
(2)由于抛物线经过E(
| 3 |
| 3 |
|
解得
|
∴抛物线的解析式为:y=-x2+2
| 3 |

(3)过M作MN∥y轴,交CE于N;
∵E(
| 3 |
| 3 |
∴直线EC:y=-
| 3 |
设M(x,-x2+2
| 3 |
| 3 |
∴MN=-x2+2
| 3 |
| 3 |
| 3 |
∴四边形EMCO的面积S=S△EMC+S△EOC
=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
=-
| ||
| 2 |
| 9 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
27
| ||
| 8 |
∴当x=
3
| ||
| 2 |
3
| ||
| 2 |
| 9 |
| 4 |
27
| ||
| 8 |
点评:此题是二次函数的综合题,涉及到图形的位似变化、二次函数解析式的确定、函数图象交点坐标及图形面积的求法、二次函数最值的应用等重要知识点,综合性强,难度较大.

练习册系列答案
相关题目
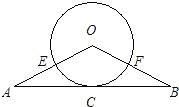 如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.

 如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F. (2013•牡丹江)如图,△ABO中,AB⊥OB,OB=
(2013•牡丹江)如图,△ABO中,AB⊥OB,OB=