题目内容
已知直线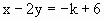 和
和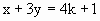 ,若它们的交点在第四象限内.
,若它们的交点在第四象限内.
(1)则k的取值范围是____<K<______;
(2)若k为非负整数,点A的坐标为(2,0),点P在直线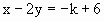 上,且
上,且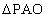 为等腰三角形,OA为底.则点P的坐标是(____,____)
为等腰三角形,OA为底.则点P的坐标是(____,____)
答案:-4,1;1,-5/2$1,-2.5
解析:
提示:
解析:
|
解: (1)直线 和 和 的交点是方程组 的交点是方程组 的解.解这个方程组,得 的解.解这个方程组,得
∵两直线的交点在第四象限 ∴  且 且
∴ 
(2)∵k为非负整数,∴由(1)得:k=0 ∴直线  为 为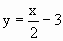
图像如图所示,过 P作 轴于E,则E是OA的中点 轴于E,则E是OA的中点
∴ E(1,0),∴P的横坐标为1将 x=1代入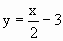 ,得 ,得
所以 P点的坐标为 . . |
提示:
(1)两直线的交点就是这两直线的解析式组成的方程组的角,它在第四象限,就是说它的横坐标大于零、纵坐标小于零; (2)P点在直线上 |

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

 阅读下面的材料:
阅读下面的材料: