摘要:设.椭圆方程为.抛物线方程为.如图6所示.过点作轴的平行线.与抛物线在第一象限的交点为.已知抛物线在点的切线经过椭圆的右焦点.(1)求满足条件的椭圆方程和抛物线方程,(2)设分别是椭圆长轴的左.右端点.试探究在抛物线上是否存在点.使得为直角三角形?若存在.请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).[解析](1)由得.当得.G点的坐标为...过点G的切线方程为即.令得.点的坐标为.由椭圆方程得点的坐标为.即.即椭圆和抛物线的方程分别为和,(2)过作轴的垂线与抛物线只有一个交点,以为直角的只有一个.同理 以为直角的只有一个.若以为直角.设点坐标为..两点的坐标分别为和. .关于的二次方程有一大于零的解.有两解.即以为直角的有两个.因此抛物线上存在四个点使得为直角三角形.
网址:http://m.1010jiajiao.com/timu_id_68947[举报]
(本小题满分14分)
设![]() ,椭圆方程为
,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() .如图6所示,过点
.如图6所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为![]() ,已知抛物线在点
,已知抛物线在点![]() 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设![]() 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).

(本小题满分14分)设![]() ,椭圆方程为
,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() .如图6所示,过点
.如图6所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为![]() ,已知抛物线在点
,已知抛物线在点![]() 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设![]() 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).

(本小题满分14分)
设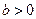 ,椭圆方程为
,椭圆方程为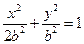 ,抛物线方程为
,抛物线方程为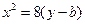 .如图6所示,过点
.如图6所示,过点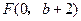 作
作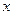 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为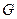 ,已知抛物线在点
,已知抛物线在点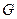 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点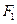 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设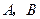 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点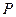 ,使得
,使得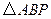 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).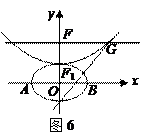
设
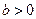 ,椭圆方程为
,椭圆方程为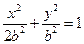 ,抛物线方程为
,抛物线方程为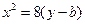 .如图6所示,过点
.如图6所示,过点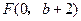 作
作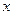 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为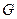 ,已知抛物线在点
,已知抛物线在点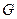 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点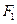 .
.(1)求满足条件的椭圆方程和抛物线方程;
(2)设
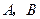 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点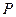 ,使得
,使得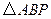 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).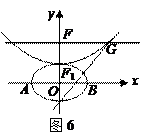
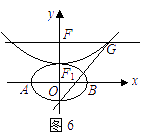
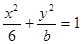 (
(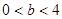 ),抛物线方程为
),抛物线方程为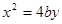 .过抛物线的焦点作
.过抛物线的焦点作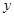 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为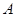 ,抛物线在点
,抛物线在点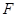 .
. 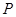 为椭圆上的动点,由
为椭圆上的动点,由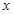 轴作垂线
轴作垂线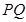 ,垂足为
,垂足为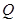 ,且直线
,且直线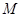 满足
满足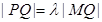 ,求点
,求点