网址:http://m.1010jiajiao.com/timu_id_68594[举报]
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).

查看习题详情和答案>>
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
【解析】第一问中利用f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
第二问中,利用当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,
即f(x1)+x1≥f(x2)+x2,结合构造函数和导数的知识来解得。
(1)f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
(2)当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,即f(x1)+x1≥f(x2)+x2,
令g(x)=f(x)+x=alnx-x2+x+1,g(x)在(0,+∞)上是减函数,
∵g′(x)= -2x+1=
-2x+1= (x>0),
(x>0),
∴-2x2+x+a≤0在x>0时恒成立,
∴1+8a≤0,a≤- ,又a<0,
,又a<0,
∴a的取值范围是
查看习题详情和答案>>
已知y=x(x-1)(x+1)的图象如图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.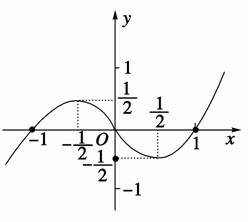
①有三个实根;
②x>1时恰有一实根;
③当0<x<1时恰有一实根;
④当-1<x<0时恰有一实根;
⑤当x<-1时恰有一实根(有且仅有一实根).
查看习题详情和答案>>仔细阅读下面问题的解法:
设A=[0, 1],若不等式21-x-a>0在A上有解,求实数a的取值范围。
解:由已知可得 a < 21-x
令f(x)= 21-x ,∵不等式a <21-x在A上有解,
∴a <f(x)在A上的最大值.
又f(x)在[0,1]上单调递减,f(x)max =f(0)=2. ∴实数a的取值范围为a<2.
研究学习以上问题的解法,请解决下面的问题:
(1)已知函数f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=![]() ,x∈A,试判断g(x)的单调性(写明理由,不必证明);
,x∈A,试判断g(x)的单调性(写明理由,不必证明);
(3)若B ={x|![]() >2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
>2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
 ) (x∈R),有下列命题:
) (x∈R),有下列命题: );
); ,0)对称;④y=f(x)的图像关于直线x=-
,0)对称;④y=f(x)的图像关于直线x=- 对称.
对称.