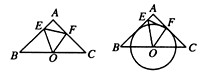摘要：(2)当∠EOF=45°时.设BE=.CF=.求与之间的函数解析式.写出的取值范围． 中的条件时.若以O为圆心的圆与AB相切.试探究直线EF与⊙O的位置关系.并证明你的的结论．
网址：http://m.1010jiajiao.com/timu_id_672176[举报]
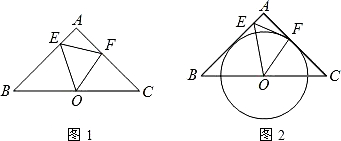
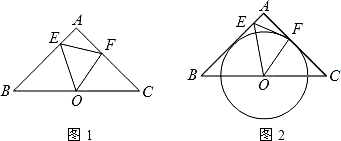
如图，已知△ABC中，AB＝AC＝2，∠A＝90°，O为BC的中点，动点E在AB边上移动，动点F在AC边上移动．
(1)点E，F的移动过程中，△OEF是否能成为∠EO
F＝45°
的等腰三角形？若能，求BE的长；若不能，请说明理由；
(2)当∠EOF＝45°时，设BE＝x，CF＝y，求y与x之间的函数解析式，并写出x的取值范围．
查看习题详情和答案>>如图，已知△ABC中，AB＝AC＝2，∠A＝90°，O为BC的中点，动点E在AB边上移动，动点F在AC边上移动．
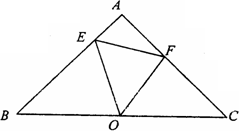
(1)点E，F的移动过程中，△OEF是否能成为∠EOF＝45°的等腰三角形？若能，求BE的长；若不能，请说明理由；
(2)当∠EOF＝45°时，设BE＝x，CF＝y，求y与x之间的函数解析式，并写出x的取值范围．
如图，在△ABC中，AB=AC=2，∠A=90°，O为BC的中点，动点E在BA边上自由移动，动点F在AC边上自由移动．
(1)点E、F的移动过程中，△OEF是否能成为∠EOF=45°的等腰三角形？若能，请指出
△OEF为等腰三角形时动点E、F的位置．若不能，请说明理由．
(2)当∠EOF=45°时，设BE=x，CF=y，求y与x之间的函数解析式，写出x的取值范围．
(3)在满足(2)中的条件时，若以O为圆心的圆与AB相切（如图），试探究直线EF与的位置关系，并证明你的结论．
(1)点E、F的移动过程中，△OEF是否能成为∠EOF=45°的等腰三角形？若能，请指出
△OEF为等腰三角形时动点E、F的位置．若不能，请说明理由．
(2)当∠EOF=45°时，设BE=x，CF=y，求y与x之间的函数解析式，写出x的取值范围．
(3)在满足(2)中的条件时，若以O为圆心的圆与AB相切（如图），试探究直线EF与的位置关系，并证明你的结论．
