Question

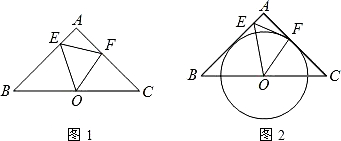
如图1所示，在△ABC中，AB=AC=2，∠A=90°，O为BC的中点，动点E在BA边上自由移动，动点F在AC边上自由移动．
（1）点E，F的移动过程中，△OEF是否能成为∠EOF=45°的等腰三角形？若能，请指出△OEF为等腰三角形时动点E，F的位置；若不能，请说明理由；
（2）当∠EOF=45°时，设BE=x，CF=y，求y与x之间的函数解析式，写出x的取值范围；
（3）在满足（2）中的条件时，若以O为圆心的圆与AB相切（如图2），试探究直线EF与⊙O的位置关系，并证明你的结论．

Answer 1

分析：（1）可分三种情况进行讨论：
①当OE=EF时；②当OF=EF时；③当OE=OF时；
（2）本题可通过图中的相似三角形BOE和CFO，可得出关于BO，OC，OE，OF的比例关系式，由于OB=OC=

2

，由此可得出关于y，x的函数关系式．
（3）要证EF是否与圆O相切，那么就要证O到EF和AB的距离是否相等．

解答：解：（1）点E，F移动的过程中，△OEF能成为∠EOF=45°的等腰三角形．
①当OE=EF时，∠OEF是直角，F，A重合，OE是三角形ABC的中位线，E是AB中点．
②当OF=EF时，∠OFE是直角，与①同理，E，A重合，F是AC中点
③当OE=OF时，如果连接OA，那么OA必然平分∠BAC，
∴BO=CO，∠B=∠C=45°，EO=FO，
因为∠EOF=45°，
∴∠BOE+∠COF=∠BOE+∠BEO=135°，
∴∠COF=∠BEO，
∴△BEO≌△COF，
∴BE=CO=

1

2

BC，
∵AB=AC=2，
∴在Rt△ABC中，BC=

AB2+AC2

=2

2

，
∴BE=CF=

2

．

（2）在△OEB和△FOC中，
∵∠EOB+∠FOC=135°，∠EOB+∠OEB=135°，
∴∠FOC=∠OEB．
又∵∠B=∠C，
∴△OEB∽△FOC．
∴

BE

CO

=

BO

CF

．
∵BE=x，CF=y，OB=OC=

1

2

22+22

=

2

，
∴y=

2

x

（1≤x≤2）．

（3）EF与⊙O相切．
∵△OEB∽△FOC，
∴

BE

CO

=

OE

OF

．
∴

BE

BO

=

OE

OF

．
即

BE

OE

=

BO

OF

．
又∵∠B=∠EOF=45°，
∴△BEO∽△OEF．
∴∠BEO=∠OEF．
∴点O到AB和EF的距离相等．
∵AB与⊙O相切，
∴点O到EF的距离等于⊙O的半径．
∴EF与⊙O相切．

点评：本题主要考查了相似三角形的性质，切线的判定等知识点，通过相似三角形得出角相等或边成比例是解题的关键．