摘要：第23题图
网址：http://m.1010jiajiao.com/timu_id_651925[举报]
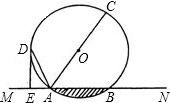如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．（1）求证：DE是⊙O的切线；
（2）若DE=6，AE=2
| 3 |
（3）在第（2）小题的条件下，则图中阴影部分的面积为
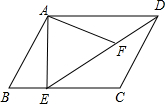如图，在平行四边形ABCD中，E为BC边上一点，且∠AED=∠B，在DE上取一点F，使AF=AE．（1）请直接写出图中所有相似的三角形（不必证明）；
（2）若AE=2
| 3 |
（可以直接使用第（1）小题结论）． 查看习题详情和答案>>
如图，直线l与⊙O相交于A，B两点，AC是⊙O的直径，D是⊙O上一点，DE⊥l于点 E，连结AD，且AD平分∠CAM．（1）求证：DE是⊙O的切线；
（2）若DE=6，AE=2
| 3 |
（3）在第（2）小题的条件下，则图中阴影部分的面积为
8π-12
| 3 |
8π-12
．| 3 |
如图是2013年某月份的月历：
星期 一 二 三 四 五 六 日
1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30 31
⑴用一个平行四边形在这张月历中任意框出四个数，设左上角第一个数为x，那么右下角的数为____________，这四个数和为_______________(用x的代数式表示) ．
⑵用上题的方法在这张月历中框出的四个数之和是否可能等于102？若有可能，请求出这四个数分别是几号；若不可能，试说明理由．
查看习题详情和答案>>利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？
如图，一个边长为1的正方形，依次取正方形的
，
，
，…
，根据图示我们可以知道：第一次取走
后还剩
，即
=1-
；前两次取走
+
后还剩
，即
+
=1-
；前三次取走
+
+
后还剩
，即
+
+
=1-
；…前
n次取走后，还剩
，即
+
+
+…
+
+
+…
=
利用上述计算：
（1）
+
+
+…+
=
（2）
+
+
+…+
=
（3）2-22-23-24-25-26-…-22011+22012 （本题写出解题过程）
查看习题详情和答案>>
如图，一个边长为1的正方形，依次取正方形的
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
n次取走后，还剩| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
1-
| 1 |
| 2n |
1-
．| 1 |
| 2n |
利用上述计算：
（1）
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
1-
| 1 |
| 3n |
1-
．| 1 |
| 3n |
（2）
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
1-
| 2n |
| 3n |
1-
．| 2n |
| 3n |
（3）2-22-23-24-25-26-…-22011+22012 （本题写出解题过程）