题目内容
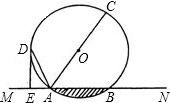 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;
(2)若DE=6,AE=2
| 3 |
(3)在第(2)小题的条件下,则图中阴影部分的面积为
分析:(1)首先由等腰三角形的性质,可得∠OAD=∠ODA,易证得DO∥MN,即可得DE⊥OD,即得DE是⊙O的切线;
(2)由勾股定理可求得AD的长,由相似三角形性质可求得AC的长,得到圆的半径;
(3)根据阴影部分的面积等于扇形面积减去等边三角形OAB的面积求解即可.
(2)由勾股定理可求得AD的长,由相似三角形性质可求得AC的长,得到圆的半径;
(3)根据阴影部分的面积等于扇形面积减去等边三角形OAB的面积求解即可.
解答: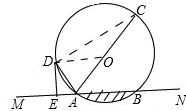 解:(1)连接OD,
解:(1)连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAM,∠OAD=∠DAE,
∴∠ODA=∠DAE,
∴DO∥MN,
∵DE⊥MN,
∴DE⊥OD,
∵D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠AED=90°,DE=6,AE=2
,
∴AD=
=
=4
,
连接CD,
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°,
∵∠CAD=∠DAE,
∴△ACD∽△ADE,
∴
=
,
∴
=
,
∴AC=8
,
∴⊙O的半径是4
;
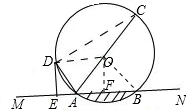
(3)过点O作OF⊥AB于F,
 ∵cos∠DAE=
∵cos∠DAE=
=
=
,
∴∠DAE=60°,
∴∠DAC=60°,
∴∠CAB=60°,
∴∠AOF=30°,
∴∠AOB=60°,
∴cos∠CAB=
=
=
,
∴AF=2
,
∴OF=6,
∴S阴影=S扇形-S△OAB=8π-12
.
 解:(1)连接OD,
解:(1)连接OD,∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAM,∠OAD=∠DAE,
∴∠ODA=∠DAE,
∴DO∥MN,
∵DE⊥MN,
∴DE⊥OD,
∵D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠AED=90°,DE=6,AE=2
| 3 |
∴AD=
| DE2+AE2 |
62+(2
|
| 3 |
连接CD,
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°,
∵∠CAD=∠DAE,
∴△ACD∽△ADE,
∴
| AD |
| AE |
| AC |
| AD |
∴
4
| ||
2
|
| AC | ||
4
|
∴AC=8
| 3 |
∴⊙O的半径是4
| 3 |
(3)过点O作OF⊥AB于F,
 ∵cos∠DAE=
∵cos∠DAE=| AE |
| AD |
2
| ||
4
|
| 1 |
| 2 |
∴∠DAE=60°,
∴∠DAC=60°,
∴∠CAB=60°,
∴∠AOF=30°,
∴∠AOB=60°,
∴cos∠CAB=
| AF |
| OA |
| AF | ||
4
|
| 1 |
| 2 |
∴AF=2
| 3 |
∴OF=6,
∴S阴影=S扇形-S△OAB=8π-12
| 3 |
点评:此题考查了圆的切线的性质与判定,以及相似三角形的判定与性质和三角函数的性质.此题综合型性比较强,解题时要注意数形结合思想的应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. (2013•路北区三模)已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.
(2013•路北区三模)已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E. 已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为
已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为 已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.
已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.