ΧβΡΩΡΎ»ί
άϊ”ΟΆΦ–Έά¥±μ Ψ ΐΝΩΜρ ΐΝΩΙΊœΒΘ§“≤Ω…“‘άϊ”Ο ΐΝΩΜρ ΐΝΩΙΊœΒά¥Οη ωΆΦ–ΈΧΊ’ςΜρΆΦ–Έ÷°ΦδΒΡΙΊœΒΘ§’β÷÷ΥΦœκΖΫΖ®≥ΤΈΣ ΐ–ΈΫαΚœΘ°Έ“Ο«Η’―ßΙΐΒΡΓΕ¥”ΟφΜΐΒΫ≥ΥΖ®ΙΪ ΫΓΖΨΆΚήΚΟΒΊΧεœ÷ΝΥ’β“ΜΥΦœκΖΫΖ®Θ§ΡψΡήάϊ”Ο ΐ–ΈΫαΚœΒΡΥΦœκΫβΨωœ¬Ν–Έ Χβ¬πΘΩ
»γΆΦΘ§“ΜΗω±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§“ά¥Έ»Γ’ΐΖΫ–ΈΒΡ
Θ§
Θ§
Θ§Γ≠
Θ§ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚΒΎ“Μ¥Έ»ΓΉΏ
ΚσΜΙ Θ
Θ§Φ¥
=1-
ΘΜ«ΑΝΫ¥Έ»ΓΉΏ
+
ΚσΜΙ Θ
Θ§Φ¥
+
=1-
ΘΜ«Α»ΐ¥Έ»ΓΉΏ
+
+
ΚσΜΙ Θ
Θ§Φ¥
+
+
=1-
ΘΜΓ≠«Α n¥Έ»ΓΉΏΚσΘ§ΜΙ Θ
n¥Έ»ΓΉΏΚσΘ§ΜΙ Θ
Θ§Φ¥
+
+
+Γ≠
+
+
+Γ≠
=
άϊ”Ο…œ ωΦΤΥψΘΚ
Θ®1Θ©
+
+
+Γ≠+
=
Θ®2Θ©
+
+
+Γ≠+
=
Θ®3Θ©2-22-23-24-25-26-Γ≠-22011+22012 Θ®±ΨΧβ–¥≥ωΫβΧβΙΐ≥ΧΘ©
»γΆΦΘ§“ΜΗω±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§“ά¥Έ»Γ’ΐΖΫ–ΈΒΡ
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
 n¥Έ»ΓΉΏΚσΘ§ΜΙ Θ
n¥Έ»ΓΉΏΚσΘ§ΜΙ Θ| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
1-
| 1 |
| 2n |
1-
Θ°| 1 |
| 2n |
άϊ”Ο…œ ωΦΤΥψΘΚ
Θ®1Θ©
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
1-
| 1 |
| 3n |
1-
Θ°| 1 |
| 3n |
Θ®2Θ©
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
1-
| 2n |
| 3n |
1-
Θ°| 2n |
| 3n |
Θ®3Θ©2-22-23-24-25-26-Γ≠-22011+22012 Θ®±ΨΧβ–¥≥ωΫβΧβΙΐ≥ΧΘ©
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨίΧβ“βΜ≠≥ωΆΦ–ΈΘ§“ά¥Έ»Γ’ΐΖΫ–ΈΟφΜΐΒΡ
Θ§
Θ§
Γ≠’“≥ωΙφ¬…Φ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΜ≠≥ωΆΦ–ΈΘ§“ά¥Έ»Γ’ΐΖΫ–ΈΟφΜΐΒΡ
Θ§
Θ§
Γ≠’“≥ωΙφ¬…Φ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΆ§ΒΉ ΐΟίΒΡ≥ΥΖ®Ϋχ––ΦΤΥψΦ¥Ω…Θ°
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
Θ®2Θ©ΗυΨίΧβ“βΜ≠≥ωΆΦ–ΈΘ§“ά¥Έ»Γ’ΐΖΫ–ΈΟφΜΐΒΡ
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
Θ®3Θ©ΗυΨίΆ§ΒΉ ΐΟίΒΡ≥ΥΖ®Ϋχ––ΦΤΥψΦ¥Ω…Θ°
Ϋβ¥πΘΚΫβΘΚΓΏΒΎ“Μ¥Έ»ΓΉΏ
ΚσΜΙ Θ
Θ§Φ¥
=1-
ΘΜ
«ΑΝΫ¥Έ»ΓΉΏ
+
ΚσΜΙ Θ
Θ§Φ¥
+
=1-
ΘΜ
«Α»ΐ¥Έ»ΓΉΏ
+
+
ΚσΜΙ Θ
Θ§Φ¥
+
+
=1-
ΘΜ
Γύ«Αn¥Έ»ΓΉΏΚσΘ§ΜΙ Θ
Θ§Φ¥
+
+
+Γ≠
=1-
ΘΜ
Ι ¥πΑΗΈΣΘΚ
Θ§
+
+
+Γ≠
=1-
ΘΜ
Θ®1Θ©»γΆΦΥυ ΨΘΚ
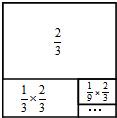
”…ΆΦΩ…÷ΣΘ§
+
+
+Γ≠+
=1-
Θ°
Ι ¥πΑΗΈΣΘΚ1-
ΘΜ
Θ®2Θ©»γΆΦ «“ΜΗω±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§ΗυΨίΆΦ Ψ

”…ΆΦΩ…÷ΣΘ§
+
+
+Γ≠+
=1-
Θ§
Ι ¥πΑΗΈΣΘΚ1-
ΘΜ
Θ®3Θ©2-22-23-24-25-26-Γ≠-22011+22012
=2-22012Θ®2-2010+2-2009+2-2008+Γ≠+2-1Θ©+22012
=2-22012Θ®1-2-2010Θ©+22012
=2-22012+4+22012
=6Θ°
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
«ΑΝΫ¥Έ»ΓΉΏ
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
«Α»ΐ¥Έ»ΓΉΏ
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
Γύ«Αn¥Έ»ΓΉΏΚσΘ§ΜΙ Θ
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
Ι ¥πΑΗΈΣΘΚ
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
Θ®1Θ©»γΆΦΥυ ΨΘΚ

”…ΆΦΩ…÷ΣΘ§
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
| 1 |
| 3n |
Ι ¥πΑΗΈΣΘΚ1-
| 1 |
| 3n |
Θ®2Θ©»γΆΦ «“ΜΗω±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§ΗυΨίΆΦ Ψ

”…ΆΦΩ…÷ΣΘ§
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
| 2n |
| 3n |
Ι ¥πΑΗΈΣΘΚ1-
| 2n |
| 3n |
Θ®3Θ©2-22-23-24-25-26-Γ≠-22011+22012
=2-22012Θ®2-2010+2-2009+2-2008+Γ≠+2-1Θ©+22012
=2-22012Θ®1-2-2010Θ©+22012
=2-22012+4+22012
=6Θ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΒΡ «’ϊ ΫΒΡΦ”ΦθΘ§ΗυΨίΧβ“βΜ≠≥ωΆΦ–ΈΘ§άϊ”Ο ΐ–ΈΫαΚœ«σΫβ «Ϋβ¥π¥ΥΧβΒΡΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΤΎΡ©1ΨμΥΊ÷ ΫΧ”ΐΤάΙάΨμœΒΝ–¥πΑΗ
ΤΎΡ©1ΨμΥΊ÷ ΫΧ”ΐΤάΙάΨμœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
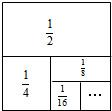
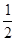 ΓΔ
ΓΔ ΓΔ
ΓΔ
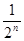 Θ§ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚ
Θ§ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚ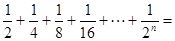 Θ°
Θ°
 Θ°
Θ° ΘΜ
ΘΜ Θ°
Θ°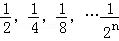 Θ§ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚΒΎ“Μ¥Έ»ΓΉΏ
Θ§ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚΒΎ“Μ¥Έ»ΓΉΏ ΚσΜΙ Θ
ΚσΜΙ Θ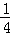 ΚσΜΙ Θ
ΚσΜΙ Θ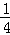 =1©¹
=1©¹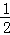 +
+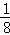 ΚσΜΙ Θ
ΚσΜΙ Θ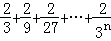 =ΓΓ_________ΓΓΘ°
=ΓΓ_________ΓΓΘ°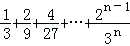 =ΓΓ_________ΓΓΘ°
=ΓΓ_________ΓΓΘ°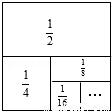
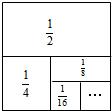
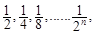 ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚΒΎ“Μ¥Έ»ΓΉΏ
ΗυΨίΆΦ ΨΈ“Ο«Ω…“‘÷ΣΒάΘΚΒΎ“Μ¥Έ»ΓΉΏ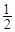 ΚσΜΙ Θ
ΚσΜΙ Θ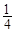 ΚσΜΙ Θ
ΚσΜΙ Θ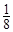 ΚσΜΙ Θ
ΚσΜΙ Θ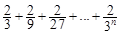 =
Θ°
=
Θ°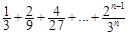 =
Θ°
=
Θ°