摘要：(1)证明:由有 .∴ .∴交点.此时二次函数为 .由②③联立.消去y.有. ∴无论m为何实数值.二次函数的图象与直线总有两个不同的交点.图代13-3-26(2)解:∵直线y=-x+m过点D.∴ -3=0+m.
网址：http://m.1010jiajiao.com/timu_id_6270[举报]
已知二次函数y=x2+ax+a-2．
（1）求证：不论a为何实数，此函数图象与x轴总有两个交点；
（2）设a＜0，当此函数图象与x轴的两个交点的距离为
时，求出此二次函数的解析式；
（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为
？若存在，求出P点坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）求证：不论a为何实数，此函数图象与x轴总有两个交点；
（2）设a＜0，当此函数图象与x轴的两个交点的距离为
| 13 |
（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为
3
| ||
| 2 |
已知二次函数y=x2+ax+a-2．
（1）求证：不论a为何实数，此函数图象与x轴总有两个交点；
（2）设a＜0，当此函数图象与x轴的两个交点的距离为
时，求出此二次函数的解析式；
（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为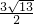
？若存在，求出P点坐标；若不存在，请说明理由．
查看习题详情和答案>>
已知二次函数y=x2+ax+a-2.
（1）求证：不论a为何实数，此函数图象与x轴总有两个交点.
（2）设a＜0，当此函数图象与x轴的两个交点A、B的距离为
时，求出此二次函数的解析式.
（3）若（2）中的条件不变，在函数图象上是否存在点P，使得△PAB的面积为
，若存在求出P点坐标，若不存在请说明理由.
查看习题详情和答案>>
（1）求证：不论a为何实数，此函数图象与x轴总有两个交点.
（2）设a＜0，当此函数图象与x轴的两个交点A、B的距离为
时，求出此二次函数的解析式. （3）若（2）中的条件不变，在函数图象上是否存在点P，使得△PAB的面积为
，若存在求出P点坐标，若不存在请说明理由. 
。
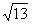时，求出此二次函数的解析式；
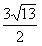，若存在求出P点坐标，若不存在请说明理由。