题目内容
已知二次函数y=x2+ax+a-2.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a<0,当此函数图象与x轴的两个交点的距离为 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为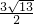 ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
解:(1)因为△=a2-4(a-2)=(a-2)2+4>0,
所以不论a为何实数,此函数图象与x轴总有两个交点.
(2)设x1、x2是y=x2+ax+a-2=0的两个根,则x1+x2=-a,x1•x2=a-2,因两交点的距离是 ,
,
所以 .
.
即:(x1-x2)2=13
变形为:(x1+x2)2-4x1•x2=13
即(-a)2-4(a-2)=13
整理得:(a-5)(a+1)=0
解方程得:a=5或-1
又∵a<0
∴a=-1
∴此二次函数的解析式为y=x2-x-3.
(3)设点P的坐标为(x0,y0),
∵函数图象与x轴的两个交点间的距离等于 ,
,
∴AB=
∴S△PAB= AB•|y0|=
AB•|y0|=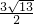
∴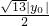 =
=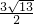
即:|y0|=3,则y0=±3
当y0=3时,x02-x0-3=3,即(x0-3)(x0+2)=0
解此方程得:x0=-2或3
当y0=-3时,x02-x0-3=-3,即x0(x0-1)=0
解此方程得:x0=0或1
综上所述,所以存在这样的P点,P点坐标是(-2,3),(3,3),(0,-3)或(1,-3).
分析:(1)由判别式△=b2-4ac可证明a为任一实数.
(2)先求出两根之和及两根之积的值,再利用两点距离公式求解.
(3)利用第2小题中两个交点的距离为 来进行计算.
来进行计算.
点评:要求熟悉二次函数与一元二次方程的关系和坐标轴上两点距离公式|x1-x2|,并熟练运用.
所以不论a为何实数,此函数图象与x轴总有两个交点.
(2)设x1、x2是y=x2+ax+a-2=0的两个根,则x1+x2=-a,x1•x2=a-2,因两交点的距离是
 ,
,所以
 .
.即:(x1-x2)2=13
变形为:(x1+x2)2-4x1•x2=13
即(-a)2-4(a-2)=13
整理得:(a-5)(a+1)=0
解方程得:a=5或-1
又∵a<0
∴a=-1
∴此二次函数的解析式为y=x2-x-3.
(3)设点P的坐标为(x0,y0),
∵函数图象与x轴的两个交点间的距离等于
 ,
,∴AB=

∴S△PAB=
 AB•|y0|=
AB•|y0|=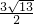
∴
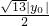 =
=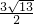
即:|y0|=3,则y0=±3
当y0=3时,x02-x0-3=3,即(x0-3)(x0+2)=0
解此方程得:x0=-2或3
当y0=-3时,x02-x0-3=-3,即x0(x0-1)=0
解此方程得:x0=0或1
综上所述,所以存在这样的P点,P点坐标是(-2,3),(3,3),(0,-3)或(1,-3).
分析:(1)由判别式△=b2-4ac可证明a为任一实数.
(2)先求出两根之和及两根之积的值,再利用两点距离公式求解.
(3)利用第2小题中两个交点的距离为
 来进行计算.
来进行计算.点评:要求熟悉二次函数与一元二次方程的关系和坐标轴上两点距离公式|x1-x2|,并熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).