摘要：∴ AD=4. 图代13-2-23(2)①无论点A在EP上怎么移动.总有.证法一:连结DB.交FH于G.∵AH是⊙O的切线.∴ ∠HDB=∠DEB.又∵BH⊥AH.BE为直径.∴ ∠BDE=90° 有 ∠DBE=90°-∠DEB =90°-∠HDB =∠DBH.在△DFB和△DHB中.DF⊥AB.∠DFB=∠DHB=90°.DB=DB.∠DBE=∠DBH.∴ △DFB∽△DHB.∴BH=BF. ∴△BHF是等腰三角形.∴BG⊥FH.即BD⊥FH.∴ED∥FH.∴.图代13-3-24证法二:连结DB.∵AH是⊙O的切线.∴ ∠HDB=∠DEF.又∵DF⊥AB.BH⊥DH.∴ ∠EDF=∠DBH.以BD为直径作一个圆.则此圆必过F.H两点.∴∠DBH=∠DFH.∴∠EDF=∠DFH.∴ ED∥FH.∴ .②∵ED=x.BH=.BH=y.BE=6.BF=BH.∴EF=6y.又∵DF是Rt△BDE斜边上的高.∴ △DFE∽△BDE.∴.即.∴.即.
网址：http://m.1010jiajiao.com/timu_id_6264[举报]
（2013•武侯区一模）（1）解不等式组：
|
（2）先化简，再求值：
| 2x |
| 4-x2 |
| 3x |
| x-2 |
| x |
| x+2 |
（3）如图，在△ABC中，∠C=90°，AC=4，∠CAB的平分线AD=
8
| ||
| 3 |
（4）若关于x、y二元一次方程组
|
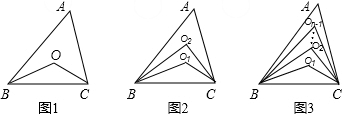
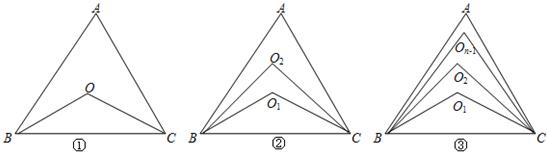
如图1，在△ABC中，∠ABC，∠ACB的角平分线交于点O，则∠BOC=90°+
∠A=
×180°+
∠A．
如图2，在△ABC中，∠ABC，∠ACB的两条三等分角线分别对应交于O1，O2，则∠BO1C=
×180°+
∠A，∠BO2C=
×180°+
∠A．
根据以上阅读理解，你能猜想（n等分时，内部有n-1个点）（用n的代数式表示）∠BOn-1C=（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图2，在△ABC中，∠ABC，∠ACB的两条三等分角线分别对应交于O1，O2，则∠BO1C=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
根据以上阅读理解，你能猜想（n等分时，内部有n-1个点）（用n的代数式表示）∠BOn-1C=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
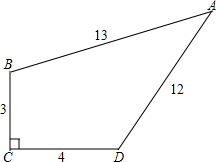
如图，四边形ABCD是平行四边形AD=12、AB=13，BD⊥AD，求OB的长及平行四边形ABCD的面积．