题目内容
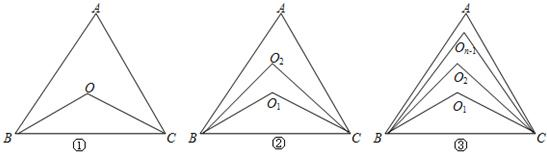
阅读下面的问题及解答.已知:如图①,在△ABC中,∠ABC、∠ACB的角平分线交于O点,则∠BOC=90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图②,在△ABC中,∠ABC、∠ACB的三等分线交于O1、O2,则∠BO1C=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
根据以上信息,回答下列问题:
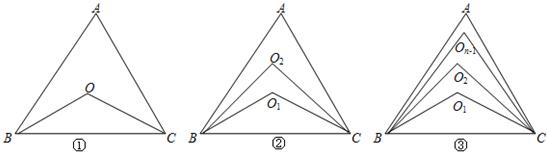
(1)你能猜想出它的规律吗?(n等分时,内部有n-1个点).∠BO1C=
∠BOn-1C=
(2)根据你的猜想,取n=4时,证明∠BO3C的度数成立.
分析:(1)根据已知中的特例,观察两部分前边的倍数和n等分线间的关系,从而写出结论;
(2)根据三角形的内角和定理和四等分角进行证明.
(2)根据三角形的内角和定理和四等分角进行证明.
解答:解:(1)∠BO1C=
×180°+
∠A,
∠BOn-1C=
×180°+
∠A.
(2)当n=4时,∠BO3C=
×180°+
∠A.
证明:等式左边=∠BO3C=180°-(∠O3BC+∠O3CB)=180°-
(∠B+∠C)
=180°-
(180°-∠A)=
×180°+
∠A=等式右边.
∴当n=4时,∠BO3C=
×180°+
∠A.
| n-1 |
| n |
| 1 |
| n |
∠BOn-1C=
| 1 |
| n |
| n-1 |
| n |
(2)当n=4时,∠BO3C=
| 1 |
| 4 |
| 3 |
| 4 |
证明:等式左边=∠BO3C=180°-(∠O3BC+∠O3CB)=180°-
| 3 |
| 4 |
=180°-
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
∴当n=4时,∠BO3C=
| 1 |
| 4 |
| 3 |
| 4 |
点评:此题综合运用了三角形的内角和定理和n等分角的概念.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB. ∠A=
∠A= ×180°+
×180°+ ∠A,∠BO2C=
∠A,∠BO2C=