题目内容
如图,∠C=90°,BC=3,CD=4,AD=12,AB=13.求这个图形的面积.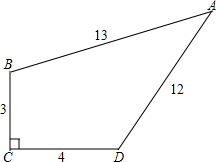
分析:连接BD.计算可知三角形ABD也是直角三角形,根据直角三角形面积公式分别计算三角形BCD和三角形ABD的面积即可.
解答:解:∵∠C=90°
∴BD=
=5,
又∵52+122=132,
故三角形ABD是直角三角形.
故三角形BCD的面积为
×3×4=6.
三角形ABD的面积为
× 5×12=30.
故这个图形的面积为30+6=36.
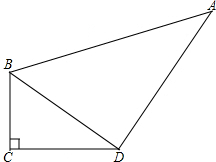
∴BD=
| 32 + 42 |
又∵52+122=132,
故三角形ABD是直角三角形.
故三角形BCD的面积为
| 1 |
| 2 |
三角形ABD的面积为
| 1 |
| 2 |
故这个图形的面积为30+6=36.

点评:本题考查了勾股定理和根据直角三角形面积公式计算直角三角形面积的能力.

练习册系列答案
相关题目
 如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )
如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )| A、AB:AC | B、AD2:DC2 | C、BD2:DC2 | D、AC2:AB2 |
 14、如图,∠AOB=90°,∠B=30°,△AOB′可以看作是由△AOB绕点O顺时针旋转α角度得到的,若点A′在AB上,则旋转角α的大小可以是
14、如图,∠AOB=90°,∠B=30°,△AOB′可以看作是由△AOB绕点O顺时针旋转α角度得到的,若点A′在AB上,则旋转角α的大小可以是 16、如图,∠C=90°,AD平分∠CAB,DE⊥AB于E,若DB=2DE=6cm,则BC=
16、如图,∠C=90°,AD平分∠CAB,DE⊥AB于E,若DB=2DE=6cm,则BC= 已知:如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,求AD.
已知:如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,求AD. 如图,∠AOB=90°,0C⊥OD,且∠BOC=
如图,∠AOB=90°,0C⊥OD,且∠BOC=