摘要:中曲线为圆锥曲线.其离心率满足.当是曲线的两个焦点时.则圆锥曲线上恒存在点.使得成立,求实数的取值范围
网址:http://m.1010jiajiao.com/timu_id_60129[举报]
一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.C 2.C 3.C 4.C 5.A 6.D 7.A 8.A 9.B
10.D 11.A 12.B
二、填空题:本大题4共小题,每小题5分。
13..files/image334.gif) 14.
14..files/image336.gif) 15.
15..files/image338.gif) 16.①④
16.①④
三、解答题(解答应写出文字说明,证明过程或演算步骤)
17.(I).files/image340.gif)
.files/image342.gif)
.files/image343.jpg) 由余弦定理得
由余弦定理得.files/image345.gif)
整理得得.files/image347.gif) 。
。
.files/image349.gif) ,故
,故.files/image138.gif) 为直角三角形
为直角三角形
(Ⅱ)设.files/image138.gif) 内角
内角.files/image353.gif) 对边的边长分别是
对边的边长分别是.files/image355.gif)
.files/image357.gif) 外接圆半径为1,
外接圆半径为1,.files/image359.gif)
.files/image361.gif)
.files/image363.gif)
.files/image365.gif) 周长的取值范围
周长的取值范围.files/image367.gif)
18.(I)证明:.files/image369.gif) ,
,
.files/image371.gif)
(Ⅱ)解:设.files/image373.gif) A
A
.files/image375.jpg)
.files/image377.gif)
设点.files/image216.gif) 到平面
到平面.files/image218.gif) 的距离为
的距离为.files/image381.gif) ,
,
.files/image383.gif)
(Ⅲ解:设.files/image385.gif) 轴建立空间直角坐标宿,为计算方便,不妨设
轴建立空间直角坐标宿,为计算方便,不妨设.files/image387.gif)
.files/image389.gif)
.files/image391.gif)
.files/image393.gif)
.files/image394.jpg) 要使二面角
要使二面角.files/image222.gif) 的大小为120°,则
的大小为120°,则.files/image397.gif)
即当.files/image399.gif) 时,二面角
时,二面角.files/image222.gif) 的大小为120°
的大小为120°
19.(I)记“厂家任意取出4件产品检验,其中至少有一件是合格品“为事件A,
则.files/image402.gif)
(Ⅱ).files/image404.gif) 的可能取值为0,1,2,
的可能取值为0,1,2,
.files/image406.gif)
所以.files/image404.gif) 的概率分布为
的概率分布为
.files/image404.gif)
0
1
2
.files/image251.gif)
.files/image411.gif)
.files/image413.gif)
.files/image415.gif)
.files/image417.gif)
20.(I)设.files/image419.gif)
.files/image421.gif)
(Ⅱ)曲线.files/image239.gif) 向左平移1一个单位,得到曲线
向左平移1一个单位,得到曲线.files/image242.gif) 的方程为
的方程为.files/image425.gif)
(1)当.files/image427.gif)
(2)当.files/image429.gif)
.files/image431.gif)
(Ⅲ).files/image433.gif)
.files/image435.gif)
21.(I).files/image437.gif)
.files/image439.gif)
(Ⅱ)令.files/image441.gif) ,
,
.files/image443.gif)
(Ⅲ)用数学归纳法证明
.files/image445.gif)
.files/image447.gif)
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分,做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑。
22..files/image449.gif)
.files/image451.gif)
23.(I).files/image453.gif) (
(.files/image315.gif) 为参数,
为参数,.files/image317.gif) 为倾斜角,且
为倾斜角,且.files/image319.gif) )
)
.files/image458.gif)
(Ⅱ).files/image460.gif)
.files/image462.gif)
24..files/image464.gif)
.files/image466.gif)
.files/image468.gif)
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:| x2 |
| 4 |
(1)过椭圆C的右焦点作一条垂直于x轴的垂轴弦MN,求MN的长度;
(2)若点P是椭圆C上不与顶点重合的任意一点,MN是椭圆C的短轴,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0)(如图),求xE?xF的值;
(3)在(2)的基础上,把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
某圆锥曲线C是椭圆或双曲线,若其中心为坐标原点,对称轴为坐标轴,且过点A(-2,2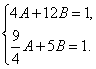 )、B(
)、B(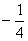 ,-
,- ),则…( )
),则…( )
A.曲线C可能为椭圆也可能为双曲线
B.曲线C一定是双曲线
C.曲线C一定是椭圆
D.这样的曲线C不存在
查看习题详情和答案>>下列关于圆锥曲线的命题:
①设A,B为两个定点,若|PA|-|PB|=2,则动点P的轨迹为双曲线;
②设A,B为两个定点,若动点P满足|PA|=10-|PB|,且|AB|=6,则|PA|的最大值为8;
③方程2x2-5x+2=0的两根可分别作椭圆和双曲线的离心率;
④双曲线
-
=1与椭圆
+y2=1有相同的焦点.
其中真命题的序号
查看习题详情和答案>>
①设A,B为两个定点,若|PA|-|PB|=2,则动点P的轨迹为双曲线;
②设A,B为两个定点,若动点P满足|PA|=10-|PB|,且|AB|=6,则|PA|的最大值为8;
③方程2x2-5x+2=0的两根可分别作椭圆和双曲线的离心率;
④双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
其中真命题的序号
②③④
②③④
(写出所有真命题的序号).