摘要：22．(1)直线AB:.∴ ①---------------------2
网址：http://m.1010jiajiao.com/timu_id_5959[举报]
直线AB过抛物线x2=2py(p＞0)的焦点9，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
(1)求证
的取值范围；
(2)过A、B两点分别作此抛物线的切线，两切线相交于N点，
求证：
；
(3)设直线AB与x轴、y轴的两个交点分别为K和L，当
=4p2，△ABN的面积的取值范围限定为[
]时，求动线段KL的轨迹所形成的平面区域的面积.
直线AB过圆心O，交圆O于A、B，直线AF交圆O于F(不与B重合)，直线l与圆O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．
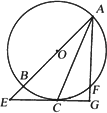
求证：(1)∠BAC＝∠CAG；
(2)AC2＝AE·AF．
直线l通过l1：x+y=2，l2：x-y=4的交点，且平分线段AB，其中A（-1，3），B（5，1），则直线l的方程是（ ）
| A、3x-y-8=0 | B、3x+y+8=0 | C、3x+y-8=0 | D、3x-y+8=0 |