题目内容
直线AB过抛物线x2=2py(p>0)的焦点9,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.(1)求证![]() 的取值范围;
的取值范围;
(2)过A、B两点分别作此抛物线的切线,两切线相交于N点,
求证:![]() ;
;
(3)设直线AB与x轴、y轴的两个交点分别为K和L,当![]() =4p2,△ABN的面积的取值范围限定为[
=4p2,△ABN的面积的取值范围限定为[![]() ]时,求动线段KL的轨迹所形成的平面区域的面积.
]时,求动线段KL的轨迹所形成的平面区域的面积.
解:由(1)条件M(0,-![]() ),F(0,
),F(0,![]() ),设直线AB的方程为
),设直线AB的方程为
y=kx+![]() ,A(x1,y1),B(x2,y2)则
,A(x1,y1),B(x2,y2)则![]() =2py1,
=2py1,![]() =2py2,Q(
=2py2,Q(![]() ).
).
由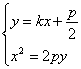 消去y并整理得x2-2pkx-p2=0.
消去y并整理得x2-2pkx-p2=0.
根据韦达定理得x1+x2=2pk,x1x2=-p2.
进而有y1y2=![]() ,
,
y1+y2=k(x1+x2)+p=2pk2+p.
∴![]() =(x1,y1+
=(x1,y1+![]() )·(x2,y2+
)·(x2,y2+![]() )
)
=x1x2+y1y2+![]() (y1+y2)+
(y1+y2)+![]()
=-p2+![]() +
+![]() (2pk2+p)+
(2pk2+p)+![]()
=p2k2≥0.
∴![]() 的取值范围是
的取值范围是![]() .
.
(2)抛物线的方程可化为y=![]() x2,求导得
x2,求导得![]() .
.
从而kNA=![]() .
.
∴切线NA的方程为y-![]() (x-x1),
(x-x1),
即y=![]() ,
,
切线NB的方程为y-![]() (x-x2),即y=
(x-x2),即y=![]() .
.
由
∴N(![]() ),
),
而x1+x2=2pk,x1x2=-p2,
∴N(pk,-![]() ).
).
而M(0,-![]() ),Q(
),Q(![]() )即(pk,pk2+
)即(pk,pk2+![]() ).
).
∴![]() =(pk,0),
=(pk,0),![]() =(0,pk2+p),
=(0,pk2+p),
又![]() =(0,
=(0,![]() ),∴
),∴![]() =0,
=0,![]() ∥
∥![]() .
.
(3)由于![]() =4p2,而根据(1)知
=4p2,而根据(1)知![]() =p2k2,
=p2k2,
∴4p2=p2k2,又p>0,∴k2=4,k=±2.
由于![]() =(-pk,p),
=(-pk,p),
![]() =(x2-x1,y2-y1)=(x2-x1,
=(x2-x1,y2-y1)=(x2-x1,![]() )
)
=(x2-x1)(1,![]() )=(x2-x1)(1,k),
)=(x2-x1)(1,k),
∴![]() =(-pk,p)·(x2-x1)(1,k)
=(-pk,p)·(x2-x1)(1,k)
=(x2-x1)(-pk+pk)=0.
从而![]() ,又
,又![]() =
=![]()
|![]() |=y1+y2+p=2pk2+2p=2p(k2+1)=10p.
|=y1+y2+p=2pk2+2p=2p(k2+1)=10p.
∴SΔABN=![]() =
=![]() .
.
而SΔABN的取值范围是[5![]() ],
],
∴![]() .
.
而p>0,所以1≤p≤2.
由(1)知直线AB的方程为y=kx+![]() ,
,
即有y=±2x+![]() ,1≤p≤2.
,1≤p≤2.
所以直线AB在x、y轴上的截距有
当k=-2,p=1时,为![]() ;
;
当k=-2,p=2时,为![]() 和1;
和1;
当k=2,p=1时,为-![]() ;
;
当k=2,p=2时,为-![]() 和1.
和1.
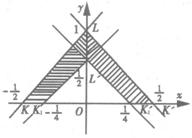
从而动线段KL的轨迹所形成的平面区域如图所示,其面积为S=S![]()
=![]()
=![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案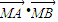 的取值范围;
的取值范围;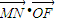 =0,
=0,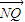 ∥
∥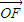 ;
;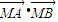 =4P2,△ABN的面积的取值范围为[5
=4P2,△ABN的面积的取值范围为[5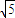 ,20
,20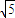 ]时,求该抛物线的方程.
]时,求该抛物线的方程.