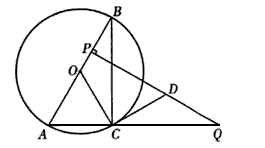
摘要：16．(1)证明:连结OC． ∵OB=OC.∠B=30°.∴∠OCB=∠B=30°．∴∠COD=∠B+∠OCB=60°．------1分∵∠BDC=30°.∴∠BDC+∠COD=90°.DC⊥OC．----------------2分∵BC是弦.∴点C是⊙O的切线．---------------------3分 ∴点C是⊙O上, ∴点BC是⊙O的切线．(2)解:∵AB=2.
网址：http://m.1010jiajiao.com/timu_id_570045[举报]
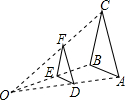如图，按如下方法将△ABC的三边缩小为原来的| 1 | 2 |
并取它们的中点D、E、F，得△EDF，下列说法：
①△ABC与△DEF是位似图形；
②△ABC与△DEF是相似图形；
③△ABC与△DEF的周长之比为2：1；
④△ABC与△DEF的面积比为4：1．
其中正确的有
①②③④
①②③④
．
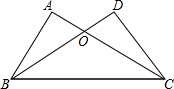如图，∠A=∠D=90゜，AC=DB，欲证OB=OC，可以先利用“HL”说明△ABC≌△DCB
△ABC≌△DCB
得到AB=DC，再利用“AAS”
“AAS”
证明△AOB≌△DOC
△DOC
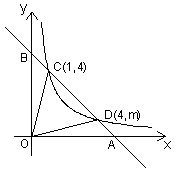
得到OB=OC．如图，已知C、D是双曲线y=
在第一象线内的分支的两点，直线CD分别交x轴、y轴于A、B两点，设C、D的坐标分别是（x1，y1）、（x2，y2）连结OC、OD．
在第一象线内的分支的两点，直线CD分别交x轴、y轴于A、B两点，设C、D的坐标分别是（x1，y1）、（x2，y2）连结OC、OD． 
（1）求证：y1＜OC＜
；
（2）若∠BOC=∠AOD=α，作DM⊥x轴于M，
=
，OC=OD=
，求直线CD的解析式；
（3）在（2）的条件下，双曲线上是否存在一点P，使得S△POD=S△POC？若存在，请给出证明；若不存在，请说明理由．
查看习题详情和答案>>
；（2）若∠BOC=∠AOD=α，作DM⊥x轴于M，
=，OC=OD=，求直线CD的解析式；（3）在（2）的条件下，双曲线上是否存在一点P，使得S△POD=S△POC？若存在，请给出证明；若不存在，请说明理由．
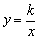的图象交于第一象限C，D两点，坐 标轴交于A、B两点，连结OC，OD（O是坐标原点）。
