摘要：其中:绕原点的旋转变换矩阵和切变变换矩阵比较难于记忆.绕原点旋转旋转θ角的变换矩阵为(特点:主对角线相同.副对角线互为相反熟.各列的平方和为1),水平切变变换矩阵为.竖直切变变换矩阵为.这些可以归结为一个歌诀: 各种变换思一般.一图二组矩阵换.(先作图.再列出方程组.最后变成矩阵形式表示) 主角相同副相反.各列平方和一旋. 副角一零一系数.主角全一是切变. 左乘矩阵变后点.参数方法求曲线.(求一个点的变换后的点是左乘矩阵,求曲线变换后方程可以设原来曲线上点为参数.再进行变换.但要注意参数的范围)
网址：http://m.1010jiajiao.com/timu_id_569412[举报]
（1）选修4-4：矩阵与变换
已知曲线C1：y=
绕原点逆时针旋转45°后可得到曲线C2：y2-x2=2，
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
，求曲线C1依次经过矩阵M1，M2对应的变换T1，T2变换后得到的曲线方程．
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
（θ为参数）上求一点，使它到直线l的距离最小，并求出该点坐标和最小距离．
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．
查看习题详情和答案>>
已知曲线C1：y=
| 1 |
| x |
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
|
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
|
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．
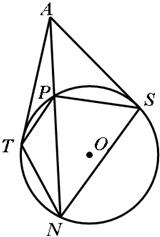选做题A．平面几何选讲