题目内容
 选做题A.平面几何选讲
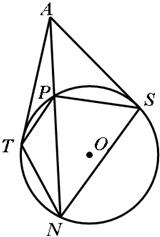
选做题A.平面几何选讲过圆O外一点A作圆O的两条切线AT、AS,切点分别为T、S,过点A作圆O的割线APN,
证明:
| AT2 |
| AN2 |
| PT•PS |
| NT•NS |
B.矩阵与变换(10分)
已知直角坐标平面xOy上的一个变换是先绕原点逆时针旋转45°,再作关于x轴反射变换,求这个变换的逆变换的矩阵.
C.坐标系与参数方程
已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
| π |
| 6 |
已知m,n是正数,证明:
| m3 |
| n |
| n3 |
| m |
分析:A、由题意过圆O外一点A作圆O的两条切线AT、AS,切点分别为T、S,过点A作圆O的割线APN,只要证明△ATN∽△APT和△ASN∽△APS,利用比例关系即可证明;
B、利用旋转变换公式直接代入即可得变换的逆变换的矩阵;
C、先将曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
)上的动点,化为一般方程 x2+(y-6)2=62,然后利用圆的几何关系进行求解;
D、不等式两边同乘mn,然后利用作差法进行化简求解;
B、利用旋转变换公式直接代入即可得变换的逆变换的矩阵;
C、先将曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
| π |
| 6 |
D、不等式两边同乘mn,然后利用作差法进行化简求解;
解答:解:A、∵AT为圆O的切线,
∴∠ATP=∠ANT,∵∠APT=∠PTN+∠ANT,∠ATN=∠ATP+∠PTN
∴∠ATN=∠APT,∴△ATN∽△APT,∴
=
=
,
∴同理可得△ASN∽△APS,∴
=
=
,
∴
=
=
=
即证;
B、这个变换的逆变换是关于x轴反射变换,再作绕原点顺时针旋转
变换,其矩阵为
=
C、∵ρ=12sinθ∴ρ2=12ρsinθ 可化为:x2+y2=12y,∴x2+(y-6)2=62
是以(0,6)为圆心 半径是6的圆.设圆心为O1
同理 ρ=12cosθ x2+y2=12x 是以(6,0)为圆心,半径为6的圆
而ρ=12cos(θ-
)相当于把坐标轴逆时针旋转了
就是30度.
把圆心从极坐标θ=0旋转到了θ=
,圆心到原点距离仍然是6.
可得圆心坐标是(3
,3)记为O2
把O1,O2的连线,和圆A,圆B分别交于D,E
容易求出它们位置是 D(-3
,9)E(6
,0)且O1在圆B上,O2在圆A上
那么DE是就是AB的最大值,
假设圆B上不同于E点的另一点F.
则 O1F<O1E (O1E是圆B的直径)
所以AF=O1F+R=O1F+6<O1E+6=12+6=18
就是Q点只能取点E,才能让AB取最大值18.此时A也只能在D点.
因为任何圆P上非D点的点G,都有GE<GO2+EO2<DO2+EO2=18,
∴线段AB长的最大值为18.
C、∵m,n是正数,证明:
+
≥m2+n2.两边同乘mn,得
m4+n4≥m3n+n3m,m,n>0
作差得,m4+n4-m3n-n3m=m3(m-n)+n3(n-m)=(m3-n3)(m-n)=(m-n)2(m2+mn+n2)≥0,
∴
+
≥m2+n2.
∴∠ATP=∠ANT,∵∠APT=∠PTN+∠ANT,∠ATN=∠ATP+∠PTN
∴∠ATN=∠APT,∴△ATN∽△APT,∴
| AT |
| AP |
| AN |
| AT |
| TN |
| PT |
∴同理可得△ASN∽△APS,∴
| AS |
| AP |
| AN |
| AS |
| SN |
| PS |
∴
| TN•SN |
| PT•PS |
| AT•AS |
| AP2 |
| AT2 | ||
|
| AN2 |
| AT2 |
B、这个变换的逆变换是关于x轴反射变换,再作绕原点顺时针旋转
| π |
| 4 |
|
|
|
C、∵ρ=12sinθ∴ρ2=12ρsinθ 可化为:x2+y2=12y,∴x2+(y-6)2=62
是以(0,6)为圆心 半径是6的圆.设圆心为O1
同理 ρ=12cosθ x2+y2=12x 是以(6,0)为圆心,半径为6的圆
而ρ=12cos(θ-
| π |
| 6 |
| π |
| 6 |
把圆心从极坐标θ=0旋转到了θ=
| π |
| 6 |
可得圆心坐标是(3
| 3 |
把O1,O2的连线,和圆A,圆B分别交于D,E
容易求出它们位置是 D(-3
| 3 |
| 3 |
那么DE是就是AB的最大值,
假设圆B上不同于E点的另一点F.
则 O1F<O1E (O1E是圆B的直径)
所以AF=O1F+R=O1F+6<O1E+6=12+6=18
就是Q点只能取点E,才能让AB取最大值18.此时A也只能在D点.
因为任何圆P上非D点的点G,都有GE<GO2+EO2<DO2+EO2=18,
∴线段AB长的最大值为18.
C、∵m,n是正数,证明:
| m3 |
| n |
| n3 |
| m |
m4+n4≥m3n+n3m,m,n>0
作差得,m4+n4-m3n-n3m=m3(m-n)+n3(n-m)=(m3-n3)(m-n)=(m-n)2(m2+mn+n2)≥0,
∴
| m3 |
| n |
| n3 |
| m |
点评:此题是一道综合题,考查了旋切角的性质,极坐标与一般方程之间的转化,以及不等式的证明,用到了作差法来求解,综合性强,但是每个小题都不是很难,做题时要有耐心,一步一步往下做,不要因为题量大就放弃.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
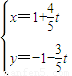 (t为参数)被曲线
(t为参数)被曲线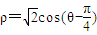 所截的弦长为 .
所截的弦长为 . (t为参数)被曲线
(t为参数)被曲线 所截的弦长为 .
所截的弦长为 .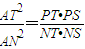 .
.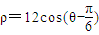 上的动点,试求线段AB长的最大值.D.不等式选讲
上的动点,试求线段AB长的最大值.D.不等式选讲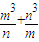 ≥m2+n2.
≥m2+n2.