摘要:解:结合图象及函数的意义可得D.
网址:http://m.1010jiajiao.com/timu_id_566960[举报]
已知函数f(x)=sin(ωx+
)(x∈R),且f(
)=1.
(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得y=
sin
x的图象;
(3)在(1)的前提下,设α∈[
,
,β∈(-
,-
),f(α)=
,f(β)=-
,
①求tanα的值;
②求cos2(α-β)-1的值. 查看习题详情和答案>>
| π |
| 3 |
| π |
| 6 |
(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得y=
| 1 |
| 2 |
| 1 |
| 2 |
(3)在(1)的前提下,设α∈[
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
①求tanα的值;
②求cos2(α-β)-1的值. 查看习题详情和答案>>
已知函数f(x)=sin(ωx+ )(x∈R),且
)(x∈R),且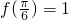 .
.
(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得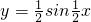 的图象;
的图象;
(3)在(1)的前提下,设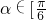 ,
, ,
,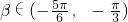 ,
,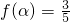 ,f(β)=-
,f(β)=- ,
,
①求tanα的值;
②求cos2(α-β)-1的值.
查看习题详情和答案>>
已知函数f(x)=sin(ωx+
)(x∈R),且f(
)=1.
(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得y=
sin
x的图象;
(3)在(1)的前提下,设α∈[
,
,β∈(-
,-
),f(α)=
,f(β)=-
,
①求tanα的值;
②求cos2(α-β)-1的值.
查看习题详情和答案>>
| π |
| 3 |
| π |
| 6 |
(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得y=
| 1 |
| 2 |
| 1 |
| 2 |
(3)在(1)的前提下,设α∈[
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
①求tanα的值;
②求cos2(α-β)-1的值.
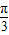 )(x∈R),且
)(x∈R),且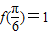 .
.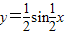 的图象;
的图象;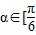 ,
,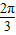 ,
,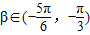 ,
,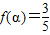 ,f(β)=-
,f(β)=- ,
,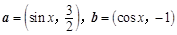 .
.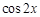 的值;
的值;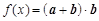 ,问:由函数
,问:由函数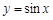 的图象经过怎样的变换可得函数
的图象经过怎样的变换可得函数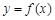 的图象?
的图象?