摘要:③ 当k=0时.方程(1)的解为-1.+1.±.方程(2)的解为x=0.原方程恰有5个不同的实根
网址:http://m.1010jiajiao.com/timu_id_566943[举报]
已知函数f(x)=![]() (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)若当x∈(-3,2)时,有不等式![]() 恒成立,求k的取值范围.
恒成立,求k的取值范围.
已知函数![]() ,其中e为自然对数的底数
,其中e为自然对数的底数
(Ⅰ)若函数g(x)在点(1,g(1))处的切线与直线2x-y+1=0垂直,求实数a的值;
(Ⅱ)若f(x)在[-1,1]上是单调增函数,求实数a的取值范围;
(Ⅲ)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
设平面向量![]() (其中
(其中![]() ),且
),且![]() .
.
(1)求函数y=f(x)的表达式;
(2)若函数y=f(x)对任意![]() 都有(x1-x2)[f(x1)-f(x2)]>0,求此时
都有(x1-x2)[f(x1)-f(x2)]>0,求此时![]() 在[1,+∞]上的最小值;
在[1,+∞]上的最小值;
(3)若点(x0,f(x0))在不等式![]() 所表示的区域内,且x0为方程
所表示的区域内,且x0为方程![]() 的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
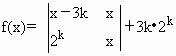 (x∈R,k为正整数)
(x∈R,k为正整数)