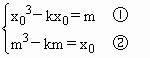题目内容
设平面向量![]() (其中
(其中![]() ),且
),且![]() .
.
(1)求函数y=f(x)的表达式;
(2)若函数y=f(x)对任意![]() 都有(x1-x2)[f(x1)-f(x2)]>0,求此时
都有(x1-x2)[f(x1)-f(x2)]>0,求此时![]() 在[1,+∞]上的最小值;
在[1,+∞]上的最小值;
(3)若点(x0,f(x0))在不等式![]() 所表示的区域内,且x0为方程
所表示的区域内,且x0为方程![]() 的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
答案:
解析:
解析:
|
解:(1)∵ ∵ ∴ ∴ (2)已知对任意的 ∴当 ∴ ∴ (3)设 ∴ 由①-②得 ∵ ∴ ∴ |

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目