网址:http://m.1010jiajiao.com/timu_id_55945[举报]
一、


二、13. ;14.
;14. ;15.
;15. ;16.
;16. 或
或 .
.
详细参考答案:
1.∵ ,∴
,∴  ,又∵
,又∵  ,∴
,∴ 
 ,选择B
,选择B
2.∵

 ,∴
,∴  ,选择D
,选择D
3.因为阴影部分在集 中又在集
中又在集 中,所阴影部分是
中,所阴影部分是 ,选择A
,选择A
4.∵ 的定义域是
的定义域是  ,∴
,∴
 ,选择C
,选择C
5.∵ ,∴选择A
,∴选择A
6.由映射的定义:A、B、C不是映射,D是映射.
7.∵ 在
在 上是减函数,∴
上是减函数,∴ ,即
,即
8. ,或
,或
 或
或 ,即
,即
9.当 时,则
时,则 ,由当
,由当 时,
时, 得,
得, ,又
,又 是奇函数,
是奇函数, ,所以
,所以 ,即
,即

10.∵
 ,
,

∴ 

 ,选择A
,选择A
11.在A中,由 图像看
图像看 ,直线应与
,直线应与 轴的截距
轴的截距 ;在B图中,
;在B图中, 经过
经过 是错误的;在D中,
是错误的;在D中, 经过
经过 是错误的,选择C
是错误的,选择C
12.根据奇函数图像关于原点对称,作出函数图像,则不等式 解
解 为
为
 ,或
,或 ,所以选择D
,所以选择D
13.∵ 是偶函数,∴
是偶函数,∴ ,∴
,∴
 的增函数区间是
的增函数区间是
14.∵ ,
, ,且
,且 ,
, ,∴
,∴ ,
, ,则
,则


15.∵ 在区间
在区间 上是奇函数,∴
上是奇函数,∴ ,∴
,∴ 在区间
在区间 上的最小值为
上的最小值为
 16.函数图像如图,方程
16.函数图像如图,方程 等价于
等价于 ,或
,或
 或
或 .
.
17.解:∵ ,
, ,
,
∴
 ,
,
 ,---------6分
,---------6分
∵ ,
, ,
,
∴  ,--------------8分
,--------------8分
∴ 
 .-------------------12分
.-------------------12分
18.解:(1)∵ ,∴
,∴  与
与 的对应法则不同,值域也不同,因此是不同的函数;
的对应法则不同,值域也不同,因此是不同的函数;
(2)∵ ,∴
,∴  与
与 的定义域不同,值域也不同,因此是不同的函数;
的定义域不同,值域也不同,因此是不同的函数;
(3)∴  与
与 的定义域相同,对应法则相同,值域也相同,因此是同一的函数.
的定义域相同,对应法则相同,值域也相同,因此是同一的函数.
19.解:∵ ,∴
,∴  ,以下分
,以下分 或
或 讨论:------------4分
讨论:------------4分
(i)
若 时,则
时,则 ;------------7分
;------------7分
(ii)
若 时,则
时,则 .--------11分
.--------11分
综上所述:实数 的取值范围是
的取值范围是 .-------------------12分
.-------------------12分
20.解:(1) 是偶函数.∵
是偶函数.∵  的定义域是
的定义域是 ,设任意
,设任意 ,都有
,都有 ,∴
,∴ 是偶函数.-----------5分
是偶函数.-----------5分
(2)函数 在
在 上是增函数.设任意
上是增函数.设任意 ,
, ,且
,且 时,
时,

 ,
,
∵  ,∴
,∴  ,
, ,
, ,
,
∴
 , 即
, 即  ,-----------------11分
,-----------------11分
故函数 在
在 上是增函数.----------------------12分
上是增函数.----------------------12分
21.解:(1)∵  ,
, ,-----------2分
,-----------2分
又  ---------①
---------①
∴  ,
,
即  ---------②-----------3分
---------②-----------3分
由①、② 得: ,
, ,-----------5分
,-----------5分
(2) ,----------6分
,----------6分
(i)当 时,函数
时,函数 的最小值为
的最小值为 ;-----8分
;-----8分
(ii)当 时,函数
时,函数 的最小值为
的最小值为 ;---10分
;---10分
(iii)当 时,函数
时,函数 的最小值为
的最小值为 .------12分
.------12分
22.解:(1)依题意有: ,即
,即 ……①,(i)当
……①,(i)当 时,方程①无解,∴当
时,方程①无解,∴当 时,无迭代不动点;(ii)当
时,无迭代不动点;(ii)当 时,方程①有无数多解,∴当
时,方程①有无数多解,∴当 时,也无迭代不动点;(iii)当
时,也无迭代不动点;(iii)当 时,方程①有唯一解
时,方程①有唯一解 有迭代不动点
有迭代不动点 .-------------6分
.-------------6分
(2)设 ,显然
,显然 时,不满足关系式,于是
时,不满足关系式,于是 ,则:
,则:
 .------8分
.------8分
有
……
 即:
即: ,比较对应的系数:
,比较对应的系数: 解之:
解之: ,所以
,所以 .----------14分.
.----------14分.
(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为
| 2 |
(2)关于x的不等式(x-1)2>f(x)的解集中的整数恰有3个,求实数a的取值范围;
(3)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=
| ||
| 2 |
(1)将函数y=f(x)图象向右平移一个单位即可得到函数y=φ(x)的图象,试写出y=φ(x)的解析式及值域;
(2)关于x的不等式(x-1)2>f(x)的解集中的整数恰有3个,求实数a的取值范围;
(3)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=
| ||
| 2 |
设函数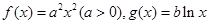 .
.
(1)若函数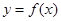 图像上的点到直线
图像上的点到直线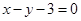 距离的最小值为
距离的最小值为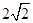 ,求
,求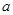 的值;
的值;
(2)关于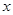 的不等式
的不等式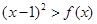 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数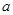 的取值范围;
的取值范围;
(3)对于函数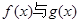 定义域上的任意实数
定义域上的任意实数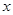 ,若存在常数
,若存在常数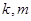 ,使得
,使得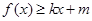 和
和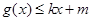 都成立,则称直线
都成立,则称直线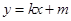 为函数
为函数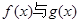 的
的
“分界线”.设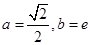 ,试探究
,试探究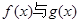 是否存在“分界线”?若存在,求出“分界线”的方程,若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程,若不存在,请说明理由.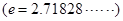
查看习题详情和答案>>
(12分) 设函数 (
(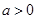 ),
), .
.
(1) 将函数 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数 的图象,试写出
的图象,试写出 的解析式及值域;
的解析式及值域;
(2) 关于 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数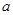 的取值范围;
的取值范围;
(3) 对于函数 与
与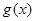 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 与
与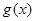 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究 与
与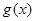 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看习题详情和答案>>
| |||||