网址:http://m.1010jiajiao.com/timu_id_546658[举报]
一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
A
B
C
D
C
B
D
二、填空题:本大题主要考查基本知识和基本运算.本大题共5小题,考生作答4小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11. 12.
12. 13.
13. 14.
14. 15.2
15.2
说明:第14题答案可以有多种形式,如可答 或
或 Z)等, 均给满分.
Z)等, 均给满分.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:(1)∵


 .
6分
.
6分
∴ .
8分
.
8分
(2) 当 时,
时,  取得最大值, 其值为2 . ……………………10分
取得最大值, 其值为2 . ……………………10分
此时 ,即
,即
 Z
Z . ……………………12分
. ……………………12分
17. (本小题满分12分)
解:(1) 由频率分布条形图知,抽取的学生总数为 人. ………… 3分
人. ………… 3分
∵各班被抽取的学生人数成等差数列,设其公差为 ,
,
由 =100,解得
=100,解得 . …………………………………… 6分
. …………………………………… 6分
∴各班被抽取的学生人数分别是22人,24人,26人,28人. …… 8分
(2) 在抽取的学生中,任取一名学生, 则分数不小于90分的概率为0.35+0.25+0.1+0.05=0.75. ………………………………12分
18.(本小题满分14分)
解:(1)∵  ⊥平面
⊥平面 ,
,
 平面
平面 ,
,
∴
 ⊥
⊥ .
………………………………………………2分
.
………………………………………………2分
∵
 ⊥
⊥ ,
,


 ,
,
∴
 ⊥平面
⊥平面 , ……………………………………………………4分
, ……………………………………………………4分
∵

 平面
平面 ,
,
∴
 ⊥
⊥ . …………………………………………………………6分
. …………………………………………………………6分
 (2)法1: 取线段
(2)法1: 取线段 的中点
的中点 ,
, 的中点
的中点 ,连结
,连结 ,
,
则 是△
是△ 中位线.
中位线.
∴ ∥
∥ ,
, , …………………………8分
, …………………………8分
∵
 ,
, ,
,
∴ .
.
∴
四边形 是平行四边形, …………………………10分
是平行四边形, …………………………10分
∴  .
.
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 . …………………………………… 13分
. …………………………………… 13分
∴
线段 的中点
的中点 是符合题意要求的点. ……………………………………14分
是符合题意要求的点. ……………………………………14分
法2: 取线段 的中点
的中点 ,
, 的中点
的中点 ,连结
,连结 ,
,
 则
则 是△
是△ 的中位线.
的中位线.
∴ ∥
∥ ,
, , …………………………8分
, …………………………8分
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 .
.
∵
 ,
, ,
,
∴ .
.
∴
四边形 是平行四边形, ……………………………………10分
是平行四边形, ……………………………………10分
∴  .
.
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 .
.
∵ ,
,
∴平面 平面
平面 .……………………………………………………12分
.……………………………………………………12分
∵ 平面
平面 ,
,
∴ ∥平面
∥平面 .
.
∴
线段 的中点
的中点 是符合题意要求的点.……………………………… 14分
是符合题意要求的点.……………………………… 14分
19. (本小题满分14分)
解:(1)依题意知, …………………………………………2分
…………………………………………2分
∵ ,
,
∴ . ………………………………………… 5分
. ………………………………………… 5分
∴所求椭圆 的方程为
的方程为 . …………………………………………6分
. …………………………………………6分
(2)∵ 点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
∴ 
解得: ,
, .
…………………………8分
.
…………………………8分
∴ .
……………………………10分
.
……………………………10分
∵
点
 在椭圆
在椭圆 :
: 上,
上,
∴ , 则
, 则 .………………………………………………12分
.………………………………………………12分
∴ 的取值范围为
的取值范围为 . …………………………………………14分
. …………………………………………14分
20. (本小题满分14分)
(1) 解:当 时,
时, .
……………………………………1分
.
……………………………………1分
当 时,
时,

 .
…………………………………………4分
.
…………………………………………4分
∵ 不适合上式,
不适合上式,
∴ ………………………………………………………5分
………………………………………………………5分
(2)证明: ∵ .
.
当 时,
时, ………………………………………………6分
………………………………………………6分
当 时,
时, ,
①
,
①
 . ②
. ②
①-②得:


得 , …………………………………………10分
, …………………………………………10分
此式当 时也适合.
时也适合.
∴ N
N .
.
∵ ,
,
∴ .
…………………………………………………11分
.
…………………………………………………11分
当 时,
时, ,
,
∴ .
.
∵ ,
,
∴ .
.
故 ,即
,即 . ……………………………………………13分
. ……………………………………………13分
综上, .
………………………………14分
.
………………………………14分
21. (本小题满分14分)
解:(1)当 时,
时, ,
,
∴
 .
.
令 =0, 得
=0, 得  .
………………………………………………2分
.
………………………………………………2分
当 时,
时, , 则
, 则 在
在 上单调递增;
上单调递增;
当 时,
时, , 则
, 则 在
在 上单调递减;
上单调递减;
当 时,
时, ,
,  在
在 上单调递增.
…………………………2分
上单调递增.
…………………………2分
∴ 当 时,
时,  取得极大值为
取得极大值为
 ;…………………………4分
;…………………………4分
当 时,
时,  取得极小值为
取得极小值为
 . ………………………6分
. ………………………6分
(2) ∵  =
=  ,
,
∴△=  =
=  .
.
① 若a≥1,则△≤0,
∴ ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0) ,
, ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. ……………………9分
② 若a<1,则△>0,
∴ = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
当 变化时,
变化时, 的取值情况如下表:
的取值情况如下表:
x

x1
(x1,x2)
x2


+
0
-
0
+
f(x)
ㄊ
极大值
ㄋ
极小值
ㄊ
∵ ,
,
∴ .
.
∴



 .
.
同理
 .
.
∴


 .
.
令f(x1)?f(x2)>0, 解得a> .
.
而当 时,
时, ,
,
故当 时, 函数f(x)的图象与x轴有且只有一个交点.
时, 函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是 .
……………………………………14分
.
……………………………………14分



⑴求数列
 的通项公式;
的通项公式;⑵设
 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;⑶是否存在以
 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
 的通项公式为
的通项公式为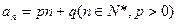 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。