网址:http://m.1010jiajiao.com/timu_id_540001[举报]
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
A
D
C
D
B
C
A
二、填空题(每小题4分,共24分)
11 数学理科.files/image245.gif) 12 10 13 144
12 10 13 144数学理科.files/image247.gif) 14
14 数学理科.files/image249.gif) 15
15 数学理科.files/image251.gif)
16 540
三、 解答题(共76分,以下各题文累积得分,其他解法请相应给分)
17解:(I)由题意得数学理科.files/image253.gif) ,即
,即数学理科.files/image255.gif) ,
,数学理科.files/image257.gif) ,……3分
,……3分
又数学理科.files/image259.gif) ,
,数学理科.files/image261.gif) ,……4分
,……4分
数学理科.files/image263.gif) ……6分
……6分
(II)数学理科.files/image265.gif) ,
,
数学理科.files/image267.gif) 于是
于是数学理科.files/image269.gif)
又数学理科.files/image271.gif) ……8分
……8分
又数学理科.files/image273.gif) ……10分
……10分
数学理科.files/image275.gif) ……12分
……12分
18 解:(I) 最大编号数学理科.files/image277.gif) 分别为3,4,5,6。
分别为3,4,5,6。数学理科.files/image279.gif) ,……2分
,……2分
数学理科.files/image281.gif) ……4分
……4分
数学理科.files/image283.gif) ,……6分
,……6分 数学理科.files/image285.gif) ……8分,即分布列为
……8分,即分布列为
数学理科.files/image277.gif)
3
4
5
6
数学理科.files/image153.gif)
数学理科.files/image289.gif)
数学理科.files/image291.gif)
数学理科.files/image293.gif)
数学理科.files/image063.gif)
(II)数学理科.files/image277.gif) 的数字期望
的数字期望数学理科.files/image297.gif) ……10分
……10分
数学理科.files/image299.gif)
数学理科.files/image277.gif) 的方差
的方差
……12分
19 解:(I)证明:连结数学理科.files/image302.gif) 是长方体,
是长方体,
数学理科.files/image304.gif) 面
面数学理科.files/image149.gif)
数学理科.files/image307.jpg) 又
又数学理科.files/image309.gif) 面
面数学理科.files/image149.gif) ,
,数学理科.files/image312.gif) ,又
,又数学理科.files/image149.gif) 是正方形,
是正方形,
数学理科.files/image315.gif)
数学理科.files/image317.gif) 面
面数学理科.files/image319.gif) ,即
,即数学理科.files/image321.gif) ……3分
……3分
又数学理科.files/image323.gif) ,
,数学理科.files/image325.gif) ……6分
……6分
(II)如图,以数学理科.files/image327.gif) 为原点建系,由题意的
为原点建系,由题意的数学理科.files/image329.gif)
数学理科.files/image331.gif) ……6分
……6分
于是数学理科.files/image333.gif)
数学理科.files/image335.gif) ,设
,设数学理科.files/image337.gif) 面
面数学理科.files/image339.gif)
不妨设数学理科.files/image341.gif) 由
由数学理科.files/image343.gif)
数学理科.files/image345.gif)
……8分
设数学理科.files/image347.gif) 面
面数学理科.files/image349.gif) ,不妨设
,不妨设数学理科.files/image351.gif)
数学理科.files/image353.gif) ……9分
……9分
若数学理科.files/image355.gif) 与
与数学理科.files/image357.gif) 的夹角
的夹角数学理科.files/image359.gif) ,则
,则数学理科.files/image361.gif) ……11分
……11分
据分析二面角数学理科.files/image161.gif) 是锐角,
是锐角,数学理科.files/image364.gif) 二面角
二面角数学理科.files/image161.gif) 的余弦值是
的余弦值是数学理科.files/image367.gif) ……12分
……12分
20 解:(I)由题意知数学理科.files/image369.gif) 故
故数学理科.files/image371.gif) ……1分
……1分
又数学理科.files/image373.gif) 设椭圆中心
设椭圆中心数学理科.files/image123.gif) 关于直线
关于直线数学理科.files/image169.gif) 的对称点为
的对称点为数学理科.files/image377.gif) ,
,
于是数学理科.files/image379.gif) 方程为
方程为数学理科.files/image381.gif) ……2分
……2分
由数学理科.files/image383.gif) 得线段
得线段数学理科.files/image379.gif) 的中点为(2,-1),从而
的中点为(2,-1),从而数学理科.files/image377.gif) 的横坐标为4
的横坐标为4
故数学理科.files/image385.gif) 椭圆的方程为
椭圆的方程为数学理科.files/image387.gif) =1……4分
=1……4分
(II)由题意知直线数学理科.files/image177.gif) 存在斜率,设直线
存在斜率,设直线数学理科.files/image177.gif) 的方程为
的方程为数学理科.files/image391.gif) 并整理得
并整理得数学理科.files/image393.gif) ①……6分
①……6分
由数学理科.files/image395.gif) ,得
,得数学理科.files/image397.gif) 又
又数学理科.files/image399.gif) 不合题意
不合题意
数学理科.files/image401.gif) ……8分
……8分
设点数学理科.files/image403.gif) ,则
,则数学理科.files/image405.gif)
由①知数学理科.files/image407.gif) ……9分
……9分
直线数学理科.files/image183.gif) 方程为
方程为数学理科.files/image410.gif) ……10分
……10分
令数学理科.files/image412.gif) 得
得数学理科.files/image414.gif) ,将
,将数学理科.files/image416.gif) 代入
代入
整理得 数学理科.files/image418.gif) ,再将
,再将数学理科.files/image420.gif) ,
,数学理科.files/image422.gif) 代入计算得
代入计算得数学理科.files/image424.gif)
数学理科.files/image364.gif) 直线
直线 数学理科.files/image427.gif) 轴相交于顶点(1,0),……12分
轴相交于顶点(1,0),……12分
21解:(I)数学理科.files/image429.gif) ……2分
……2分
数学理科.files/image431.gif)
① 数学理科.files/image433.gif) 若
若数学理科.files/image435.gif) ,则当
,则当数学理科.files/image437.gif) 或
或数学理科.files/image439.gif) 时
时数学理科.files/image441.gif) 时,
时,
内是增函数,在 数学理科.files/image443.gif) 内是减函数 ,……4分
内是减函数 ,……4分
② 若数学理科.files/image445.gif)
数学理科.files/image447.gif) 内是增函数,在
内是增函数,在数学理科.files/image449.gif) 内是减函数……6分
内是减函数……6分
(II)由题意知数学理科.files/image451.gif) 得
得数学理科.files/image453.gif) ……7分
……7分
数学理科.files/image455.gif) 恰有一根(含重根 )
恰有一根(含重根 )
数学理科.files/image457.gif) ……8分
……8分
又数学理科.files/image459.gif)
数学理科.files/image461.gif) 的值域为
的值域为数学理科.files/image463.gif) 和
和数学理科.files/image465.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image468.gif) 内是增函数,
内是增函数,
由题意的数学理科.files/image470.gif) 解得
解得数学理科.files/image472.gif) ……12分
……12分
当数学理科.files/image474.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image477.gif) 内是增函数
内是增函数
由题意得数学理科.files/image479.gif) 解得
解得数学理科.files/image481.gif)
综上知实数数学理科.files/image097.gif) 的取值范围为
的取值范围为数学理科.files/image484.gif) ……14分
……14分
22 解(I)设数学理科.files/image219.gif) 公差为
公差为数学理科.files/image487.gif) ,由
,由数学理科.files/image489.gif) 得
得数学理科.files/image491.gif) ……1分
……1分
数学理科.files/image364.gif) 数列
数列数学理科.files/image217.gif) 为3,5,7,9,7,5,3,……2分
为3,5,7,9,7,5,3,……2分
(II)数学理科.files/image495.gif) ……3分
……3分
又数学理科.files/image497.gif) =
=数学理科.files/image499.gif) ……4分
……4分
数学理科.files/image501.gif)
(III)所有可能的“对称数列”是①1,2,22数学理科.files/image503.gif)
②数学理科.files/image505.gif)
③数学理科.files/image507.gif)
④数学理科.files/image509.gif) ……9分
……9分
当
数学理科.files/image511.gif)
对于②当数学理科.files/image513.gif)
当
数学理科.files/image515.gif)
对于③当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当数学理科.files/image521.gif)
数学理科.files/image523.gif) 分
分
对于④当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当
数学理科.files/image527.gif)
(本小题满分12分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2,…,xa的样本方差 ,其中
,其中 为样本平均数.
为样本平均数.
(本小题满分13分)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图:

(I)求出表中M、p及图中a的值
(II)学校决定对参加社区服务的学生进行表彰,对参加活动次数在[25,30]区间的每个学生发放价值80元的学习用品,对参加活动次数在[20,25)区间的每个学生发放价值60元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,设X为此二人所获得学习用品价值之差的绝对值,求X的分布列与数学期望E(X)。
查看习题详情和答案>>
(本小题满分12分)
某校为宣传县教育局提出的“教育发展,我的责任”教育实践活动,要举行一次以“我
为教育发展做什么”为主题的的演讲比赛,比赛分为初赛、复赛、决赛三个阶段进行,已知
某选手通过初赛、复赛、决赛的概率分别是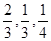 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在比赛中比赛的次数为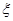 ,求
,求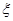 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看习题详情和答案>>
(本小题满分12分)
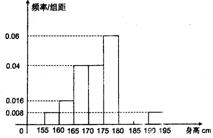
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(Ⅰ)求这组数据的众数和中位数(精确到0.1);
( II )根据有关规定,成绩小于16秒为达标.
(ⅰ)用样本估计总体,某班有学生45人,设
 为达标人数,求
为达标人数,求 的数学期望与方差.
的数学期望与方差.
(ⅱ)如果男女生使用相同的达标标准,则男女
生达标情况如下表
|
性别 是否达标 |
男 |
女 |
合计 |
|
达标 |
|
|
_____ |
|
不达标 |
|
|
_____ |
|
合计 |
______ |
______ |
|
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
查看习题详情和答案>>

 ______
______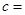 _____
_____
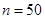
 、第二组
、第二组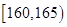 ;…第八组
;…第八组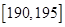 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.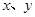 ,求满足
,求满足 的事件概率;
的事件概率;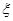 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求