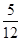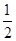题目内容
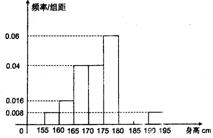
(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组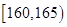 ;…第八组
;…第八组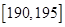 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(II)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为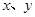 ,求满足
,求满足 的事件概率;
的事件概率;
(III)从最后三组中任取3名学生参加学校篮球队,用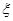 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求 的分布列及其数学期望。
的分布列及其数学期望。
(1)略(2)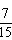 (3)
(3)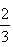
【解析】(I)由直方图知,前五组频率为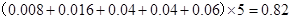 ,
,
后三组频率为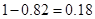 ,
,
人数为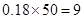 (人)………………………………2分
(人)………………………………2分
由直方图得第八组频率为:
0.008×5=0.04,
人数为0.04×50=2(人) …………2分
设第六组人数为m,则第七组人数为
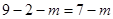 ,
,
又m+2=2(7-m),∴m=4 …………3分
所以第六组人数为4人,第七组人数为3人,频率分别等于0.08,0.06 …………4分
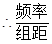 分别等于0.016,0.012,(画图如上) …………5分
分别等于0.016,0.012,(画图如上) …………5分
(II)由(I)知身高在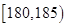 内的人数为4人,设为
内的人数为4人,设为 .
.
身高在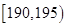 的人数为2人,设为
的人数为2人,设为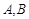 .
.
若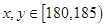 时,有
时,有 共六种情况.
共六种情况.
若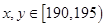 时,有
时,有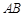 共一种情况.
共一种情况.
若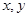 分别在
分别在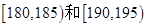 内时,
内时,
有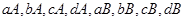 共8种情况
共8种情况
∴基本事件的总数为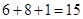 种 …………………2分
种 …………………2分
事件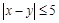 所包含的基本事件个数有
所包含的基本事件个数有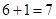 种, …………7分
种, …………7分
∴ ……………………14分
……………………14分
解法二:由(I)知身高在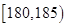 内的人数为4人,
内的人数为4人,
身高在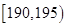 的人数为2人,
的人数为2人,
则从这两组的所有男生中随机抽取两名男生共有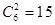 种方法,…………6分
种方法,…………6分
而事件“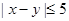 ”要求这两名男生都是第六组或者都是第八组,
”要求这两名男生都是第六组或者都是第八组,
则其包含的事件数有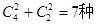 ………………7分
………………7分
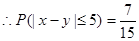 …………8分
…………8分
(III)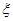 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
|
P( |
|
|
|
………………11分
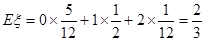 …………11分
…………11分