Question

（本小题满分12分）
某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验.选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙.
（I）假设n=4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列和数学期望；
（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm²）如下表：

分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
附：样本数据x₁，x₂，…，x_a的样本方差，其中为样本平均数.

Answer 1

解析：（I）X可能的取值为0,1,2,3,4,且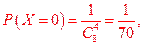
      

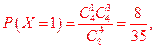
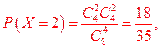
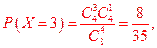
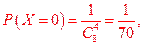
即X的分布列为

X	0	1	2	3	4
P

X的数学期望是：
.
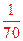
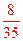
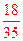
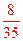
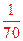
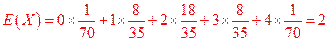（II）品种甲的每公顷产量的样本平均数和样本方差分别是：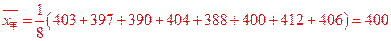
，
.
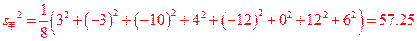品种乙的每公顷产量的样本平均数和样本方差分别是：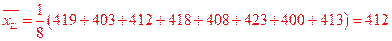
，
，
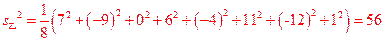由以上结果可以看出，品种乙的样本平均数大于品种甲的样本平均数，且两品种的样本方差差异不大，故应该选择种植品种乙.

解析