摘要：S△AOB＝m ? tan∠AOB.试求的最小值,的条件下.直线AB恒过一定点. 并求出此定点的坐标.
网址：http://m.1010jiajiao.com/timu_id_537277[举报]
已知函数f（x）=ax+bsinx，当x=
时，取得极小值
-
．
（1）求a，b的值；
（2）对任意x1，x2∈[-
，
]，不等式f（x1）-f（x2）≤m恒成立，试求实数m的取值范围；
（3）设直线l：y=g（x），曲线S：y=F（x），若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有g（x）≥F（x），则称直线l与曲线S的“上夹线”．观察下图：
根据上图，试推测曲线S：y=mx-nsinx（n＞0）的“上夹线”的方程，并作适当的说明．
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
| 3 |
（1）求a，b的值；
（2）对任意x1，x2∈[-
| π |
| 3 |
| π |
| 3 |
（3）设直线l：y=g（x），曲线S：y=F（x），若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有g（x）≥F（x），则称直线l与曲线S的“上夹线”．观察下图：
根据上图，试推测曲线S：y=mx-nsinx（n＞0）的“上夹线”的方程，并作适当的说明．
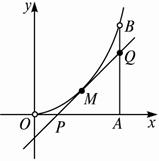
如图所示，曲线段OMB是函数?f(x)=?x2(0＜x＜6)的图象，BA⊥x轴于A点，曲线段OMB上一点M(t,f(t))的切线PQ交x轴于P点，交线段AB于Q.
(1)试用t表示切线PQ的方程;
(2)试用t表示△QAP的面积g(t),若函数g(t)在(m,n)上单调递减，试求出m的最小值;
(3)若S△QAP∈［
，64］，试求出点P横坐标的取值范围.
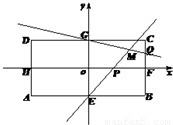
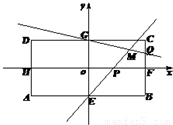
如图，在矩形ABCD中，AB=8，BC=4，E，F，G，H分别为四边的中点，且都在坐标轴上，设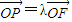
，
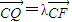（λ≠0）．
（Ⅰ）求直线EP与GQ的交点M的轨迹Γ的方程；
（Ⅱ）过圆x2+y2=r2（0＜r＜2）上一点N作圆的切线与轨迹Γ交于S，T两点，若
，试求出r的值．
查看习题详情和答案>>
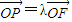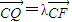，（λ≠0）．（Ⅰ）求直线EP与GQ的交点M的轨迹Γ的方程；
（Ⅱ）过圆x2+y2=r2（0＜r＜2）上一点N作圆的切线与轨迹Γ交于S，T两点，若
，试求出r的值．
查看习题详情和答案>>
，
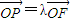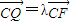（λ≠0）．
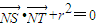，试求出r的值．