摘要：解:1.∵1=p, n=pn-1,∴n=pn.又b1=q, b2=q1+rb1=q(p+r), b3=q2+rb2=q(p2+pq+r2),-设想用数学归纳法证明:当n=2时.等式成立; 设当n=k时.等式成立.即则bk+1=qk+rbk=即n=k+1时等式也成立所以对于一切自然数n≥2.都成立
网址：http://m.1010jiajiao.com/timu_id_5370[举报]
设数列{an}的通项是关于x的不等式x2-x＜（2n-1）x （n∈N*）的解集中整数的个数．数列{an}的前n项和为Sn．
（Ⅰ）求an；
（Ⅱ）设m，k，p∈N*，m+p=2k，求证：
+
≥
；
（Ⅲ）对于（Ⅱ）中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．
查看习题详情和答案>>
（Ⅰ）求an；
（Ⅱ）设m，k，p∈N*，m+p=2k，求证：
| 1 |
| Sm |
| 1 |
| Sp |
| 2 |
| Sk |
（Ⅲ）对于（Ⅱ）中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．
已知向量
=(1，1)，向量
与向量
的夹角为
，且
•
=-1
（1）求向量
的坐标；
（2）若向量
与向量
的夹角为
，向量
=(x2，a2)，
=(a2，x)，求关于x的不等式(
+
)•
＜1的解集．
查看习题详情和答案>>
| m |
| n |
| m |
| 3π |
| 4 |
| n |
| m |
（1）求向量
| n |
（2）若向量
| n |
| i |
| π |
| 2 |
| p |
| q |
| p |
| n |
| q |
在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中a2+b2≠0且ω＞0．设f(x)=
•
．
（1）若a=
，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；
（2）若点A是过点（-1，1）且法向量为
=(-1，1)的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
，0)对称，且在x=
处f（x）取得最小值”．
查看习题详情和答案>>
| OA |
| OB |
（1）若a=
| 3 |
（2）若点A是过点（-1，1）且法向量为
| n |
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
| π |
| 3 |
| π |
| 6 |
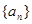的通项是关于x的不等式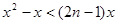
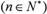的解集中整数的个数.
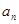并且证明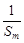
＋
≥
；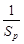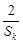