题目内容
设数列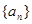 的通项是关于x的不等式
的通项是关于x的不等式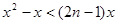
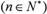 的解集中整数的个数.
的解集中整数的个数.
(1)求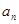 并且证明
并且证明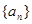 是等差数列;
是等差数列;
(2)设m、k、p∈N*,m+p=2k,求证: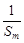 +
+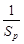 ≥
≥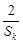 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,
请证明你的结论,如果不成立,请说明理由.
【答案】
(1)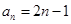 (2)见解析
(2)见解析
【解析】(1)解不等式可得 ,从而可得
,从而可得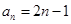 .再利用等差数列的定义证明即可.
.再利用等差数列的定义证明即可.
(2)在(1)的基础上,可求出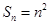 ,从而可知
,从而可知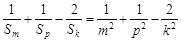 ,然后再通分利用基本不等式证明.
,然后再通分利用基本不等式证明.
(3) 设等差数列{an}的首项为a1,公差为d,则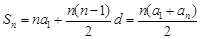 ,
,
然后再表示出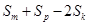 ,利用
,利用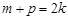 代入左边式子进行化简借助基本不等式进行证明
代入左边式子进行化简借助基本不等式进行证明

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
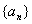 的通项是关于x的不等式
的通项是关于x的不等式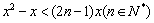 的解集中整数的个数.
的解集中整数的个数.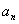 ,并且证明
,并且证明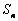 为
为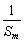 +
+ ≥
≥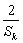 ;
;