摘要:故只需证明1+ln(x-1) ≤x-1.
网址:http://m.1010jiajiao.com/timu_id_534735[举报]
给出下列五个命题:其中正确的命题有
①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积S=
sinxdx;
②
=
+
;
③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式
+
+
+…+
>
,(n≥2,n∈N*)的过程中,由假设n=k成立推到n=k+1成立时,只需证明
+
+
+…+
+
+
>
即可.
查看习题详情和答案>>
②③④
②③④
(填序号).①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积S=
| ∫ | π -π |
②
| C | r+1 n+1 |
| C | r+1 n |
| C | r n |
③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 13 |
| 24 |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
| 13 |
| 24 |
给出下列五个命题:其中正确的命题有 (填序号).
①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积 ;
;
② ;
;
③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式 的过程中,由假设n=k成立推到n=k+1成立时,只需证明
的过程中,由假设n=k成立推到n=k+1成立时,只需证明 即可.
查看习题详情和答案>>
即可.
查看习题详情和答案>>
①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积
 ;
;②
 ;
;③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式
 的过程中,由假设n=k成立推到n=k+1成立时,只需证明
的过程中,由假设n=k成立推到n=k+1成立时,只需证明 即可.
查看习题详情和答案>>
即可.
查看习题详情和答案>>
给出下列五个命题:其中正确的命题有______(填序号).
①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积S=
sinxdx;
②
=
+
;
③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式
+
+
+…+
>
,(n≥2,n∈N*)的过程中,由假设n=k成立推到n=k+1成立时,只需证明
+
+
+…+
+
+
>
即可.
查看习题详情和答案>>
①函数y=sinx(x∈[-π,π])的图象与x轴围成的图形的面积S=
| ∫ | π-π |
②
| C | r+1n+1 |
| C | r+1n |
| C | rn |
③在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和;
④i+i2+i3+…i2012=0;
⑤用数学归纳法证明不等式
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 13 |
| 24 |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
| 13 |
| 24 |
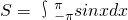 ;
;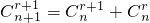 ;
;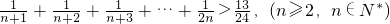 的过程中,由假设n=k成立推到n=k+1成立时,只需证明
的过程中,由假设n=k成立推到n=k+1成立时,只需证明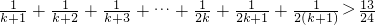 即可.
即可.