又A.P.B.Q四点共线.从而．——青夏教育精英家教网——

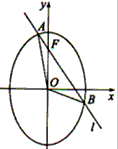
摘要：又A.P.B.Q四点共线.从而．

网址：http://m.1010jiajiao.com/timu_id_530232[举报]

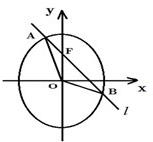已知O为坐标原点，F为椭圆C：x2+

=1在y轴正半轴上的焦点，过F且斜率为-

的直线l与C交于A、B两点，点P满足

．
（Ⅰ）证明：点P在C上；
（Ⅱ）设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上．查看习题详情和答案>>

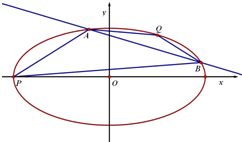如图，已知椭圆

=1上两定点P(-2，0)，Q(1，

)，直线l：y=-

x+m与椭圆相交于A，B两点（异于P，Q两点）
（1）求证：k_PA+k_QB为定值；
（2）当m∈（-1，2）时，求A、P、B、Q四点围成的四边形面积的最大值．

查看习题详情和答案>>

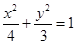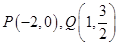如图，已知椭圆上两定点,直线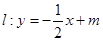与椭圆相交于A,B两点（异于P,Q两点）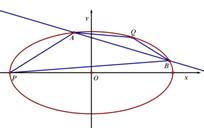

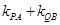（1）求证：为定值；

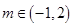（2）当时，求A、P、B、Q四点围成的四边形面积的最大值。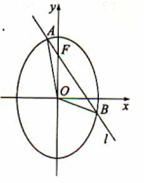

查看习题详情和答案>>

（本小题满分12分）（注意：在试题卷上作答无效）

已知O为坐标原点，F为椭圆在y轴正半轴上的焦点，过F且斜率为的直线与C交于A、B两点，点P满足

（Ⅰ）证明：点P在C上；

（Ⅱ）设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上．

查看习题详情和答案>>

已知O为坐标原点，F为椭圆C：

在y轴正半轴上的焦点，过F且斜率为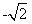

的直线l与C交与A、B两点，点P满足

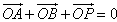（1）证明：点P在C上；
（2）设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上。

查看习题详情和答案>>