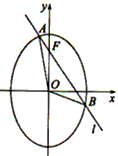
题目内容
 已知O为坐标原点,F为椭圆C:x2+
已知O为坐标原点,F为椭圆C:x2+| y2 |
| 2 |
| 2 |
| OA |
| OB |
| OP |
| 0 |
(Ⅰ)证明:点P在C上;
(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上.
分析:(1)要证明点P在C上,即证明P点的坐标满足椭圆C的方程x2+
=1,根据已知中过F且斜率为-
的直线l与C交于A、B两点,点P满足
+
+
=
,我们求出点P的坐标,代入验证即可.
(2)若A、P、B、Q四点在同一圆上,则我们可以先求出任意三点确定的圆的方程,然后将第四点坐标代入验证即可.
| y2 |
| 2 |
| 2 |
| OA |
| OB |
| OP |
| 0 |
(2)若A、P、B、Q四点在同一圆上,则我们可以先求出任意三点确定的圆的方程,然后将第四点坐标代入验证即可.
解答:证明:(Ⅰ)设A(x1,y1),B(x2,y2)
椭圆C:x2+
=1 ①,则直线AB的方程为:y=-
x+1 ②
联立方程可得4x2-2
x-1=0,
则x1+x2=
,x1×x2=-
则y1+y2=-
(x1+x2)+2=1
设P(p1,p2),
则有:
=(x1,y1),
=(x2,y2),
=(p1,p2);
∴
+
=(x1+x2,y1+y2)=(
,1);
=(p1,p2)=-(
+
)=(-
,-1)
∴p的坐标为(-
,-1)代入①方程成立,所以点P在C上.
(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上.
设线段AB的中点坐标为(
,
),即(
,
),
则过线段AB的中点且垂直于AB的直线方程为:y-
=
(x-
),即y=
x+
;③
∵P关于点O的对称点为Q,故0(0.0)为线段PQ的中点,
则过线段PQ的中点且垂直于PQ的直线方程为:y=-
x④;
③④联立方程组,解之得:x=-
,y=
③④的交点就是圆心O1(-
,
),
r2=|O1P|2=(-
-(-
))2+(-1-
)2=
故过P Q两点圆的方程为:(x+
)2+(y-
)2=
…⑤,
把y=-
x+1 …②代入⑤,
有x1+x2=
,y1+y2=1
∴A,B也是在圆⑤上的.
∴A、P、B、Q四点在同一圆上.
椭圆C:x2+
| y2 |
| 2 |
| 2 |
联立方程可得4x2-2
| 2 |
则x1+x2=
| ||
| 2 |
| 1 |
| 4 |
则y1+y2=-
| 2 |
设P(p1,p2),
则有:
| 0A |
| 0B |
| 0P |
∴
| 0A |
| 0B |
| ||
| 2 |
| 0P |
| 0A |
| 0B |
| ||
| 2 |
∴p的坐标为(-
| ||
| 2 |
(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上.
设线段AB的中点坐标为(
| x1+x2 |
| 2 |
| y1+ y2 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
则过线段AB的中点且垂直于AB的直线方程为:y-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 4 |
∵P关于点O的对称点为Q,故0(0.0)为线段PQ的中点,
则过线段PQ的中点且垂直于PQ的直线方程为:y=-
| ||
| 2 |
③④联立方程组,解之得:x=-
| ||
| 8 |
| 1 |
| 8 |
③④的交点就是圆心O1(-
| ||
| 8 |
| 1 |
| 8 |
r2=|O1P|2=(-
| ||
| 2 |
| ||
| 8 |
| 1 |
| 8 |
3
| ||
| 8 |
故过P Q两点圆的方程为:(x+
| ||
| 8 |
| 1 |
| 8 |
3
| ||
| 8 |
把y=-
| 2 |
有x1+x2=
| ||
| 2 |
∴A,B也是在圆⑤上的.
∴A、P、B、Q四点在同一圆上.
点评:本题考查的知识点是直线与圆锥曲线的关系,向量在几何中的应用,其中判断点与曲线关系时,所使用的坐标代入验证法是解答本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
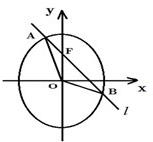
 •
• =-4,则点A的坐标是 .
=-4,则点A的坐标是 .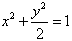 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为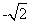 的直线l与C交于A、B两点,点P满足
的直线l与C交于A、B两点,点P满足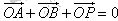 。
。