题目内容
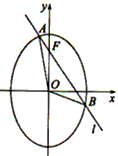
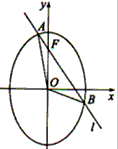
已知O为坐标原点,F为椭圆C: 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为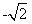 的直线l与C交与A、B两点,点P满足
的直线l与C交与A、B两点,点P满足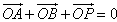 。
。
 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为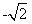 的直线l与C交与A、B两点,点P满足
的直线l与C交与A、B两点,点P满足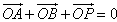 。
。
(1)证明:点P在C上;
(2)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
(2)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
解:(1)设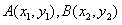
直线l: 与
与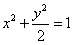 联立得
联立得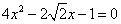
则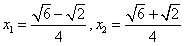

由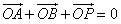 得
得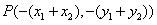
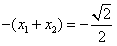

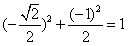
所以点P在C上。
(2)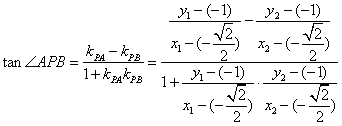
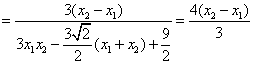
同理
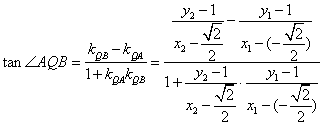
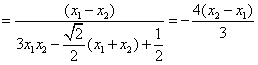
所以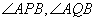 互补
互补
因此A、P、B、Q四点在同一圆上。
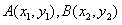
直线l:
 与
与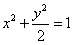 联立得
联立得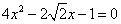
则
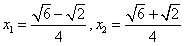

由
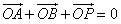 得
得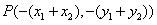
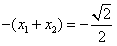

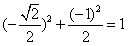
所以点P在C上。
(2)
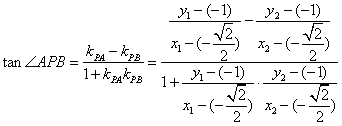
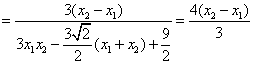
同理
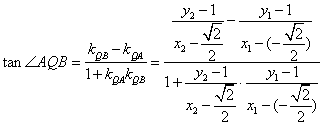
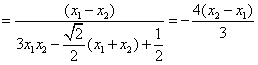
所以
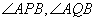 互补
互补因此A、P、B、Q四点在同一圆上。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
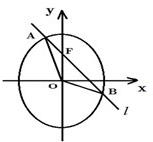 已知O为坐标原点,F为椭圆C:
已知O为坐标原点,F为椭圆C: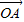 •
•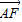 =-4,则点A的坐标是 .
=-4,则点A的坐标是 .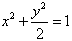 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为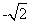 的直线l与C交于A、B两点,点P满足
的直线l与C交于A、B两点,点P满足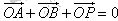 。
。