Question

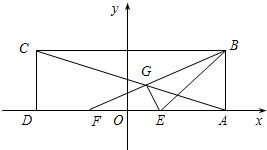在矩形ABCD中，已知AD=6，AB=2，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为⊙H．以DA所在直线为x轴，以DA中点O为坐标原点，建立如图所示的平面直角坐标系．
（1）求以F、E为焦点，DC和AB所在直线为准线的椭圆的方程．
（2）求⊙H的方程．
（3）设点P（0，b），过点P作直线与⊙H交于M，N两点，若点M恰好是线段PN的中点，求实数b的取值范围．

Answer 1

分析：（1）设出椭圆的标准方程，根据焦点坐标和准线方程求得c和

a2

c

的值，进而求得a和b，则椭圆方程可得．
（2）根据题意可知A，B，C，F的坐标，进而求得AC和BF的直线方程，联立求得焦点G的坐标，进而求得EG，BF的斜率，根据二者的乘积为-1判断出EG⊥BF，进而求得圆心和半径，进而求得圆的标准方程．
（3）设M点的坐标为（x₀，y₀），则N点的坐标可知，代入圆的方程联立求得8x₀+4（1-b）y₀+b²+2b-9=0，判断出点M在此直线上，进而根据点到直线的距离求得圆心到直线的距离小于或等于

2

整理求得b的范围．

解答：解；（1）由已知，设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，
由于焦点E的坐标为（1，0），它对应的准线方程为x=3，
所以c=1，

a2

c

=3，于是a²=3，b²=2，
所以所求的椭圆方程为：

x2

3

+

y2

2

=1．

（2）由题意可知A（3，0），B（3，2），C（-3，2），F（-1，0）．
所以直线AC和直线BF的方程分别为：x+3y-3=0，x-2y+1=0，
由

x+3y-3=0  x-2y+1=0

解得

x= 3 5   y= 4 5

所以G点的坐标为(

3

5

， 

4

5

)．
所以k_EG=-2，kBF=

1

2

，
因为k_EG•k_BF=-1，所以EG⊥BF，
所以⊙H的圆心为BE中点H（2，1），半径为BH=

2

，
所以⊙H方程为（x-2）²+（y-1）²=2．

（3）设M点的坐标为（x₀，y₀），则N点的坐标为（2x₀，2y₀-b），
因为点M，N均在⊙H上，所以

(x0-2)2+(y0-1)2=2              ① (2x0-2)2+(2y0-b-1)2=2      ②

，
由②-①×4，得8x₀+4（1-b）y₀+b²+2b-9=0，
所以点M（x₀，y₀）在直线8x+4（1-b）y+b²+2b-9=0，
又因为点M（x₀，y₀）在⊙H上，
所以圆心H（2，1）到直线8x+4（1-b）y+b²+2b-9=0的距离

|16+4(1-b)+b2+2b-9|

64+16(1-b)2

≤

2

，
即| (b-1)2+10 |≤4

8+2(b-1)2

，
整理，得（b-1）⁴-12（b-1）²-28≤0，即[（b-1）²+2][（b-1）²-14]≤0，
所以1-

14

≤b≤1+

14

，故b的取值范围为[1-

14

，1+

14

]．

点评：本题主要考查了直线与圆锥曲线的综合问题．有效地考查考生分析问题、解决问题的能力．