题目内容
已知点P在曲线C:y=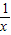 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.(Ⅰ)求f(t)的解析式;
(Ⅱ)设数列{an}(n≥1,n∈N)满足a1=1,an=
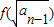 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=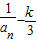 ,求an与bn;
,求an与bn;(Ⅲ)在(Ⅱ)的条件下,当1<k<3时,证明不等式:a1+a2+…+an>
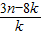 .
.
【答案】分析:(Ⅰ)先求出曲线C在点P处的切线为l的方程,求出点B的坐标,联立切线方程与方程y=kx求出点A的坐标,代入f(t)=xA•xB.就可求得f(t)的解析式;
(Ⅱ)利用(Ⅰ)的结论求出数列{an}的递推关系,再利用bn= 求出数列{bn}的递推关系,根据k的取值分别求出an与bn即可.
求出数列{bn}的递推关系,根据k的取值分别求出an与bn即可.
(Ⅲ)利用(Ⅱ)的结论求出数列{an-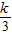 }的表达式,再对其用放缩法求和,即可证明不等式:a1+a2+…+an>
}的表达式,再对其用放缩法求和,即可证明不等式:a1+a2+…+an> .
.
解答:解:(Ⅰ)∵ ,∴
,∴ ,又点P的坐标为
,又点P的坐标为 ,
,
曲线C在点P处的切线的斜率为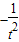 ,则切线l的方程为
,则切线l的方程为 ,
,
令y=0,得xB=2t;由 得
得 ,
,
∴ 故
故 (3分)
(3分)
(Ⅱ)由已知,n≥2时, ,得
,得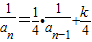 ,
,
∴ ;
;
①当k=3时,b1=0,数列{bn}是以0为首项的常数列,则bn=0,从而an=1;(5分)
②当k≠3时, ,数列{bn}为等比数列,bn=
,数列{bn}为等比数列,bn=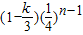 ,
,
从而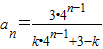
综上, ,bn=
,bn= (8分)
(8分)
(Ⅲ)
∵1<k<3,∴
∴ ,(10分)
,(10分)
∴
=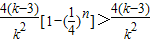 ,
,
∴ ,(12分)
,(12分)
又∵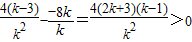 ,
,
∴ ,∴
,∴ ,即所证不等式成立.(14分)
,即所证不等式成立.(14分)
点评:本题涉及到用放缩法来证明不等式.当函数与数列,不等式合在一起出题时,多会涉及到用放缩法来证明不等式.在放缩时,放缩的度要把握好.
(Ⅱ)利用(Ⅰ)的结论求出数列{an}的递推关系,再利用bn=
 求出数列{bn}的递推关系,根据k的取值分别求出an与bn即可.
求出数列{bn}的递推关系,根据k的取值分别求出an与bn即可.(Ⅲ)利用(Ⅱ)的结论求出数列{an-
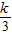 }的表达式,再对其用放缩法求和,即可证明不等式:a1+a2+…+an>
}的表达式,再对其用放缩法求和,即可证明不等式:a1+a2+…+an> .
.解答:解:(Ⅰ)∵
 ,∴
,∴ ,又点P的坐标为
,又点P的坐标为 ,
,曲线C在点P处的切线的斜率为
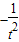 ,则切线l的方程为
,则切线l的方程为 ,
,令y=0,得xB=2t;由
 得
得 ,
,∴
 故
故 (3分)
(3分)(Ⅱ)由已知,n≥2时,
 ,得
,得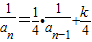 ,
,∴
 ;
;①当k=3时,b1=0,数列{bn}是以0为首项的常数列,则bn=0,从而an=1;(5分)
②当k≠3时,
 ,数列{bn}为等比数列,bn=
,数列{bn}为等比数列,bn=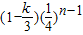 ,
,从而
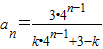
综上,
 ,bn=
,bn= (8分)
(8分)(Ⅲ)

∵1<k<3,∴

∴
 ,(10分)
,(10分)∴

=
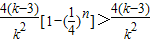 ,
,∴
 ,(12分)
,(12分)又∵
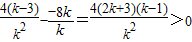 ,
,∴
 ,∴
,∴ ,即所证不等式成立.(14分)
,即所证不等式成立.(14分)点评:本题涉及到用放缩法来证明不等式.当函数与数列,不等式合在一起出题时,多会涉及到用放缩法来证明不等式.在放缩时,放缩的度要把握好.

练习册系列答案
相关题目
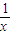 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.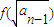 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=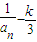 ,求an与bn;
,求an与bn;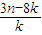 .
.