摘要:(10)提示:过直线任作一平面的是任意的.所以这样的平面有无数对.
网址:http://m.1010jiajiao.com/timu_id_510152[举报]
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
查看习题详情和答案>>
已知椭圆C1:
+
=1(a>b>0)的右焦点与抛物线C2:y2=4x的焦点F重合,点M是C1与C2在第一象限内的交点,且|MF|=
.
(1)求椭圆C1的方程;
(2)设抛物线的准线与x轴交于点E,过E任作一条直线l,l与椭圆C1的两个交点记为A,B.问:在椭圆的长轴上是否存在一点P,使
•
为定值?若存在,求出点P的坐标及相应的定值;若不存在,请说明理由.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
(1)求椭圆C1的方程;
(2)设抛物线的准线与x轴交于点E,过E任作一条直线l,l与椭圆C1的两个交点记为A,B.问:在椭圆的长轴上是否存在一点P,使
| PA |
| PB |
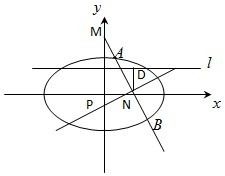
(2013•威海二模)已知椭圆
+
=1(a>b>0)的离心率为e=
,过右焦点做垂直于x轴的直线与椭圆相交于两点,且两交点与椭圆的左焦点及右顶点构成的四边形面积为
+2.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点M(0,2),直线l:y=1,过M任作一条不与y轴重合的直线与椭圆相交于A、B两点,若N为AB的中点,D为N在直线l上的射影,AB的中垂线与y轴交于点P.求证:
为定值.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
2
| ||
| 3 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点M(0,2),直线l:y=1,过M任作一条不与y轴重合的直线与椭圆相交于A、B两点,若N为AB的中点,D为N在直线l上的射影,AB的中垂线与y轴交于点P.求证:
| ||||
|
 (2013•威海二模)已知椭圆
(2013•威海二模)已知椭圆