Question

（2013•威海二模）已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为e=

6

3

，过右焦点做垂直于x轴的直线与椭圆相交于两点，且两交点与椭圆的左焦点及右顶点构成的四边形面积为

2 6

3

+2．
（Ⅰ）求椭圆的标准方程；
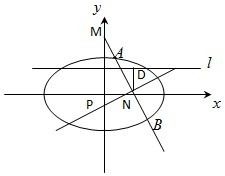
（Ⅱ）设点M（2，0），直线l：y=1，过M任作一条不与y轴重合的直线l₁与椭圆相交于A、B两点，过AB的中点N作直线l₂与y轴交于点P，D为N在直线l上的射影，若|ND|、

1

2

|AB|、|MP|成等比数列，求直线l₂的斜率的取值范围．

Answer 1

分析：（Ⅰ）由e=

6

3

得

c

a

=

6

3

，由过右焦点做垂直于x轴的直线与椭圆相交于两点，且两交点与椭圆的左焦点及右顶点构成的四边形面积为

2 6

3

+2，得（a+c）•

b2

a

=

2 6

3

+2，结合a²=b²+c²求得a，b的值，则椭圆方程可求；
（Ⅱ）设l₁的斜率为k₁，l₂的斜率为k₂，写出直线l₁的方程，和椭圆方程联立后由判别式大于0求出k的范围，利用根与系数关系得到A，B两点的横坐标的和与积，代入弦长公式求|AB|，利用中点坐标公式求出N的坐标，写出NP所在直线方程，求出P点坐标，则|ND|、|MP|的长度可求，由|ND|、

1

2

|AB|、|MP|成等比数列得到k₁，k₂的关系，由k₁的范围可得k₂的范围．

解答：解：（Ⅰ）由题意可得

c a = 6 3 (a+c)• b2 a = 2 6 3 +2 a2=b2+c2

，解得

a= 6 b= 2

．
所以椭圆标准方程为

x2

6

+

y2

2

=1；
（Ⅱ）设l₁的斜率为k₁，l₂的斜率为k₂，直线l₁的方程为y=k₁x+2，
A（x₁，y₁），B（x₂，y₂），联立直线与椭圆方程

y=k1x+2 x2 6 + y2 2 =1

，整理得(3k12+1)x2+12k1x+6=0．
∵直线l₁与椭圆由两个公共点，∴△=(12k1)2-4(3k12+1)•6＞0?3k12-1＞0．
∴k1＜-

3

3

或k1＞

3

3

．
由x1+x2=

-12k1

3k12+1

，x1x2=

6

3k12+1

，
得|AB|²=(1+k12)[(x1+x2)2-4x1x2]=(1+k12)[

144k12

(3k12+1)

-

24

1+3k12

]
=

24(1+k12)(3k12-1)

(1+3k12)2

．
设N（x^′，y^′），则x′=

x1+x2

2

=

-6k1

3k12+1

，y′=k1x′+2=

2

3k12+1

．
∴直线NP的方程为y-

2

1+3k12

=k2(x+

6k1

1+3k12

)，令x=0，得yp=

6k1k2+2

1+3k12

，
∴|ND|=|1-

2

1+3k12

|=

(3k12-1)

1+3k12

，|MP|=|2-

6k1k2+2

1+3k12

|=|

6k12-6k1k2

1+3k12

|．
∵|ND|、

1

2

|AB|、|MP|成等比数列，则有|AB|²=4|MC|•|ND|
∴

24(1+k12)(3k12-1)

(1+3k12)2

=4

(3k12-1)

1+3k12

|

6k12-6k1k2

1+3k12

|
1+k12=|k12-k1k2|，则1+k12=k12-k1k2或1+k12=k1k2-k12
∴k2=-

1

k1

或k2=2k1+

1

k1

．
由k2=-

1

k1

，可得k2∈(-

3

，0)∪(0，

3

)
由k2=2k1+

1

k1

，可得k2∈(-∞，-2

2

]∪[2

2

，+∞)
∴k₂的取值范围为(-∞，-2

2

]∪[2

2

，+∞)∪(-

3

，0)∪(0，

3

)．

点评：本题考查了椭圆的标准方程，考查了直线与圆锥曲线的关系，训练了“设而不求”的解题方法，考查了分类讨论的解题思想和数学转化思想方法，考查了学生的运算能力，是难题．