摘要:所以不等式的解集是 ---14分
网址:http://m.1010jiajiao.com/timu_id_504925[举报]
(本小题满分14分)在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点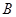 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
.
(I)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(II)若点 是曲线
是曲线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若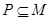 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(III)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在 处
处 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
查看习题详情和答案>>
(本小题满分14分)在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且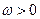 .设
.设 .
.
(I)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(II)若点 是曲线
是曲线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(III)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点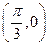 对称,且在
对称,且在 处
处 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且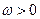 .设
.设 .
.(I)若
 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;(II)若点
 是曲线
是曲线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;(III)根据本题条件我们可以知道,函数
 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点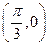 对称,且在
对称,且在 处
处 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】选做题(请考生在下列两题中任选一题作答,若两题都做,则接所做的第一题计分)
(l)(坐标系与参数方程选做题)在直角坐标系xoy中,曲线C1参数方程
(a为参数),在极坐标系(与直角坐标系xoy相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为p(cosθ-sinθ)+1=0,则曲线C1与 C2的交点个数为
(2)(不等式选做题)若关于x的不等式ax2-|x-1|+2a<0的解集为空集,则a的取值范围是
查看习题详情和答案>>
(l)(坐标系与参数方程选做题)在直角坐标系xoy中,曲线C1参数方程
|
2
2
.(2)(不等式选做题)若关于x的不等式ax2-|x-1|+2a<0的解集为空集,则a的取值范围是
a≥
| ||
| 4 |
a≥
.
| ||
| 4 |
本题共有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则以所做的前2题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
变换T1是逆时针旋转90°的旋转变换,对应的变换矩阵为M1,变换T2对应的变换矩阵是 ;
;
(I)求点P(2,1)在T1作用下的点Q的坐标;
(II)求函数y=x2的图象依次在T1,T2变换的作用下所得的曲线方程.
(2)选修4-4:极坐标系与参数方程
从极点O作一直线与直线l:ρcosθ=4相交于M,在OM上取一点P,使得OM•OP=12.
(Ⅰ)求动点P的极坐标方程;
(Ⅱ)设R为l上的任意一点,试求RP的最小值.
(3)选修4-5:不等式选讲
已知f(x)=|6x+a|.
(Ⅰ)若不等式f(x)≥4的解集为 ,求实数a的值;
,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x-1)>b对一切实数x恒成立,求实数b的取值范围.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
变换T1是逆时针旋转90°的旋转变换,对应的变换矩阵为M1,变换T2对应的变换矩阵是
 ;
;(I)求点P(2,1)在T1作用下的点Q的坐标;
(II)求函数y=x2的图象依次在T1,T2变换的作用下所得的曲线方程.
(2)选修4-4:极坐标系与参数方程
从极点O作一直线与直线l:ρcosθ=4相交于M,在OM上取一点P,使得OM•OP=12.
(Ⅰ)求动点P的极坐标方程;
(Ⅱ)设R为l上的任意一点,试求RP的最小值.
(3)选修4-5:不等式选讲
已知f(x)=|6x+a|.
(Ⅰ)若不等式f(x)≥4的解集为
 ,求实数a的值;
,求实数a的值;(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x-1)>b对一切实数x恒成立,求实数b的取值范围.
查看习题详情和答案>>
本题共有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则以所做的前2题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
变换T1是逆时针旋转90°的旋转变换,对应的变换矩阵为M1,变换T2对应的变换矩阵是M2=
;
(I)求点P(2,1)在T1作用下的点Q的坐标;
(II)求函数y=x2的图象依次在T1,T2变换的作用下所得的曲线方程.
(2)选修4-4:极坐标系与参数方程
从极点O作一直线与直线l:ρcosθ=4相交于M,在OM上取一点P,使得OM•OP=12.
(Ⅰ)求动点P的极坐标方程;
(Ⅱ)设R为l上的任意一点,试求RP的最小值.
(3)选修4-5:不等式选讲
已知f(x)=|6x+a|.
(Ⅰ)若不等式f(x)≥4的解集为{x|x≥
或x≤-
},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x-1)>b对一切实数x恒成立,求实数b的取值范围.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
变换T1是逆时针旋转90°的旋转变换,对应的变换矩阵为M1,变换T2对应的变换矩阵是M2=
|
(I)求点P(2,1)在T1作用下的点Q的坐标;
(II)求函数y=x2的图象依次在T1,T2变换的作用下所得的曲线方程.
(2)选修4-4:极坐标系与参数方程
从极点O作一直线与直线l:ρcosθ=4相交于M,在OM上取一点P,使得OM•OP=12.
(Ⅰ)求动点P的极坐标方程;
(Ⅱ)设R为l上的任意一点,试求RP的最小值.
(3)选修4-5:不等式选讲
已知f(x)=|6x+a|.
(Ⅰ)若不等式f(x)≥4的解集为{x|x≥
| 1 |
| 2 |
| 5 |
| 6 |
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x-1)>b对一切实数x恒成立,求实数b的取值范围.