题目内容
本题共有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则以所做的前2题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.(1)选修4-2:矩阵与变换
变换T1是逆时针旋转90°的旋转变换,对应的变换矩阵为M1,变换T2对应的变换矩阵是
 ;
;(I)求点P(2,1)在T1作用下的点Q的坐标;
(II)求函数y=x2的图象依次在T1,T2变换的作用下所得的曲线方程.
(2)选修4-4:极坐标系与参数方程
从极点O作一直线与直线l:ρcosθ=4相交于M,在OM上取一点P,使得OM•OP=12.
(Ⅰ)求动点P的极坐标方程;
(Ⅱ)设R为l上的任意一点,试求RP的最小值.
(3)选修4-5:不等式选讲
已知f(x)=|6x+a|.
(Ⅰ)若不等式f(x)≥4的解集为
 ,求实数a的值;
,求实数a的值;(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x-1)>b对一切实数x恒成立,求实数b的取值范围.
【答案】分析:(1)求出M1,可得点P(2,1)在T1作用下的点Q的坐标.设变换为M,则M=M2M1=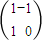 ,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),根据
,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),根据 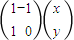 =
= ,可得x=x-y,x=y,再由
,可得x=x-y,x=y,再由
又y=x2,得到 y-x=y2.
(2)设动点P的极坐标(ρ,θ),点M的极坐标为(ρ,θ),则ρρ=12,可得ρ=3cosθ (扣除极点).
根据P的轨迹是以(1.5,0)为圆心,以1.5为半径的圆,得RP的最小值为1.
(3)由|6x+a|≥4 解得x≥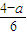 ,或 x≤
,或 x≤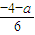 ,从而
,从而 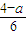 =
= ,
,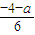 =-
=- ,解得 a=1,求出f(x)
,解得 a=1,求出f(x)
的解析式,求出f(x)+f(x-1)的最小值为12,可得b<12.
解答:(1)解:(Ⅰ)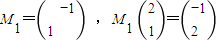 ,点P(2,1)在T1作用下的点Q的坐标为(-1,2).…4分
,点P(2,1)在T1作用下的点Q的坐标为(-1,2).…4分
(II)设变换为M,则M=M2M1=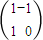 ,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),
,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),
则有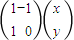 =
=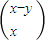 ,∴x=x-y,x=y.
,∴x=x-y,x=y.
又y=x2,∴y-x=y2.
(2)解:(Ⅰ)设动点P的极坐标(ρ,θ),点M的极坐标为(ρ,θ),则ρρ=12.
又ρcosθ=4,∴ρ=3cosθ (扣除极点).
(Ⅱ)由(Ⅰ)知,动点P的轨迹是以(1.5,0)为圆心,以1.5为半径的圆,故RP的最小值为1.
(3)解:由|6x+a|≥4 解得x≥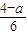 ,或 x≤
,或 x≤ ,∴
,∴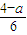 =
= ,
,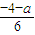 =-
=- ,
,
解得 a=1. 此时,f(x)=|6x+1|,f(x+1)=|6x+7|,f(x-1)=|6x-5|.
f(x)+f(x-1)=|6x+7|+|6x-5|≥|(6x+7)-(6x-5)|=12,故b<12.
点评:本题考查矩阵运算,简单曲线的极坐标方程,函数的恒成立问题,是一道基础题.
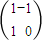 ,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),根据
,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),根据 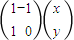 =
= ,可得x=x-y,x=y,再由
,可得x=x-y,x=y,再由又y=x2,得到 y-x=y2.
(2)设动点P的极坐标(ρ,θ),点M的极坐标为(ρ,θ),则ρρ=12,可得ρ=3cosθ (扣除极点).
根据P的轨迹是以(1.5,0)为圆心,以1.5为半径的圆,得RP的最小值为1.
(3)由|6x+a|≥4 解得x≥
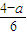 ,或 x≤
,或 x≤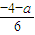 ,从而
,从而 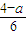 =
= ,
,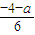 =-
=- ,解得 a=1,求出f(x)
,解得 a=1,求出f(x)的解析式,求出f(x)+f(x-1)的最小值为12,可得b<12.
解答:(1)解:(Ⅰ)
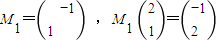 ,点P(2,1)在T1作用下的点Q的坐标为(-1,2).…4分
,点P(2,1)在T1作用下的点Q的坐标为(-1,2).…4分(II)设变换为M,则M=M2M1=
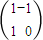 ,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),
,设(x,y)是变换后曲线上的任意一点,与之对应的变换前的点是(x,y),则有
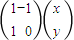 =
=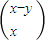 ,∴x=x-y,x=y.
,∴x=x-y,x=y.又y=x2,∴y-x=y2.
(2)解:(Ⅰ)设动点P的极坐标(ρ,θ),点M的极坐标为(ρ,θ),则ρρ=12.
又ρcosθ=4,∴ρ=3cosθ (扣除极点).
(Ⅱ)由(Ⅰ)知,动点P的轨迹是以(1.5,0)为圆心,以1.5为半径的圆,故RP的最小值为1.
(3)解:由|6x+a|≥4 解得x≥
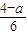 ,或 x≤
,或 x≤ ,∴
,∴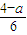 =
= ,
,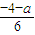 =-
=- ,
,解得 a=1. 此时,f(x)=|6x+1|,f(x+1)=|6x+7|,f(x-1)=|6x-5|.
f(x)+f(x-1)=|6x+7|+|6x-5|≥|(6x+7)-(6x-5)|=12,故b<12.
点评:本题考查矩阵运算,简单曲线的极坐标方程,函数的恒成立问题,是一道基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 ,并且矩阵M对应的变换将点(-1,2)变换成(9,15).求矩阵M.
,并且矩阵M对应的变换将点(-1,2)变换成(9,15).求矩阵M. (α是参数).
(α是参数).