题目内容
(本小题满分14分)在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且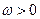 .设
.设 .
.
(I)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(II)若点 是曲线
是曲线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(III)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点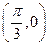 对称,且在
对称,且在 处
处 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且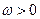 .设
.设 .
.(I)若
 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;(II)若点
 是曲线
是曲线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;(III)根据本题条件我们可以知道,函数
 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点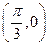 对称,且在
对称,且在 处
处 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】(I) 在
在 内的解集为
内的解集为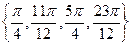
(II) 的最大值
的最大值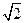 .
.
(III)使得函数 满足“图像关于点
满足“图像关于点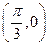 对称,且在
对称,且在 处
处 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当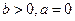 时,
时,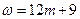 (
(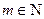 )或当
)或当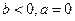 时,
时,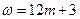 (
(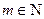 )”.
)”.
 在
在 内的解集为
内的解集为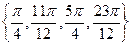
(II)
 的最大值
的最大值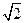 .
. (III)使得函数
 满足“图像关于点
满足“图像关于点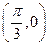 对称,且在
对称,且在 处
处 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当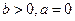 时,
时,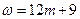 (
(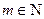 )或当
)或当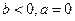 时,
时,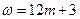 (
(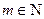 )”.
)”.解:(I)由题意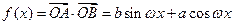 ,…………………………1分
,…………………………1分
当 ,
, ,
, 时,
时,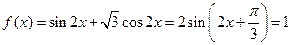 ,…2分
,…2分
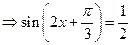 ,则有
,则有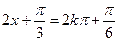 或
或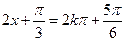 ,
,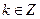 .
.
即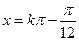 或
或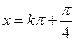 ,
,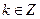 . ……………4分
. ……………4分
又因为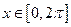 ,故
,故 在
在 内的解集为
内的解集为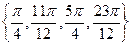 .……5分
.……5分
(II)由题意, 是曲线
是曲线 上的动点,故
上的动点,故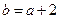 . ……………6分
. ……………6分
因此,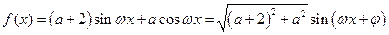 ,
,
所以, 的值域
的值域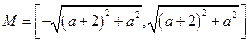 . ……………8分
. ……………8分
又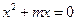 的解为0和
的解为0和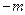 ,故要使
,故要使 恒成立,只需
恒成立,只需
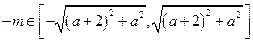 ,而
,而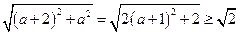 ,
,
即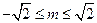 ,所以
,所以 的最大值
的最大值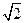 . …………………10分
. …………………10分
(III)解:因为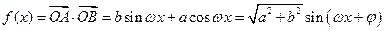 ,
,
设周期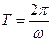 .
.
由于函数 须满足“图像关于点
须满足“图像关于点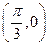 对称,且在
对称,且在 处
处 取得最小值”.
取得最小值”.
因此,根据三角函数的图像特征可知,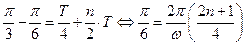
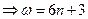 ,
,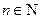 .
.
又因为,形如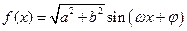 的函数的图像的对称中心都是
的函数的图像的对称中心都是 的零点,故需满足
的零点,故需满足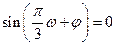 ,而当
,而当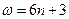 ,
,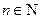 时,
时,
因为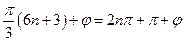 ,
,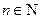 ;所以当且仅当
;所以当且仅当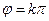 ,
,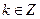 时,
时, 的图像关于点
的图像关于点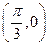 对称;此时,
对称;此时,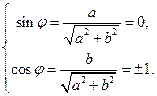
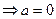 ,
,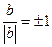 .
.
(i)当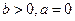 时,
时,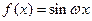 ,进一步要使
,进一步要使 处
处 取得最小值,则有
取得最小值,则有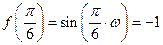
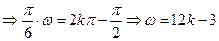 ,
,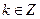 ;又
;又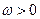 ,则有
,则有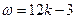 ,
,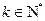 ;因此,由
;因此,由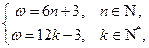 可得
可得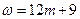 ,
,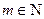 ;
;
(ii)当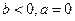 时,
时,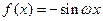 ,进一步要使
,进一步要使 处
处 取得最小值,则有
取得最小值,则有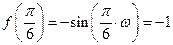
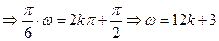 ,
,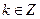 ;又
;又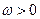 ,则有
,则有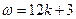 ,
,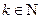 ;因此,由
;因此,由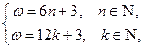 可得
可得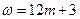 ,
,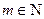 ;
;
综上,使得函数 满足“图像关于点
满足“图像关于点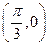 对称,且在
对称,且在 处
处 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当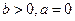 时,
时,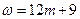 (
(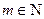 )或当
)或当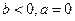 时,
时,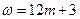 (
(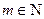 )”. ……………………………………………………14分
)”. ……………………………………………………14分
(第III小题将根据学生对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分)
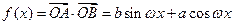 ,…………………………1分
,…………………………1分当
 ,
, ,
, 时,
时,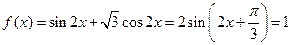 ,…2分
,…2分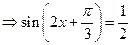 ,则有
,则有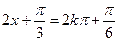 或
或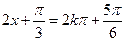 ,
,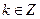 .
.即
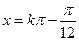 或
或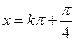 ,
,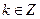 . ……………4分
. ……………4分又因为
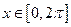 ,故
,故 在
在 内的解集为
内的解集为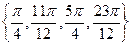 .……5分
.……5分(II)由题意,
 是曲线
是曲线 上的动点,故
上的动点,故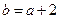 . ……………6分
. ……………6分因此,
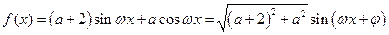 ,
,所以,
 的值域
的值域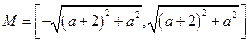 . ……………8分
. ……………8分又
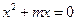 的解为0和
的解为0和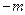 ,故要使
,故要使 恒成立,只需
恒成立,只需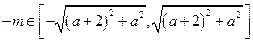 ,而
,而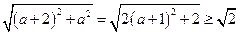 ,
,即
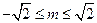 ,所以
,所以 的最大值
的最大值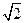 . …………………10分
. …………………10分(III)解:因为
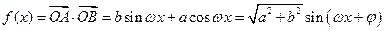 ,
,设周期
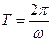 .
.由于函数
 须满足“图像关于点
须满足“图像关于点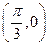 对称,且在
对称,且在 处
处 取得最小值”.
取得最小值”.因此,根据三角函数的图像特征可知,
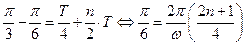
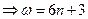 ,
,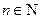 .
.又因为,形如
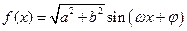 的函数的图像的对称中心都是
的函数的图像的对称中心都是 的零点,故需满足
的零点,故需满足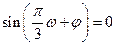 ,而当
,而当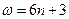 ,
,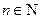 时,
时,因为
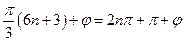 ,
,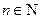 ;所以当且仅当
;所以当且仅当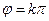 ,
,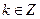 时,
时, 的图像关于点
的图像关于点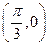 对称;此时,
对称;此时,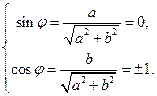
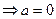 ,
,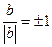 .
.(i)当
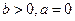 时,
时,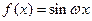 ,进一步要使
,进一步要使 处
处 取得最小值,则有
取得最小值,则有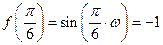
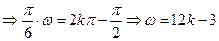 ,
,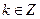 ;又
;又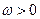 ,则有
,则有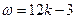 ,
,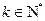 ;因此,由
;因此,由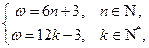 可得
可得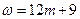 ,
,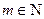 ;
;(ii)当
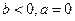 时,
时,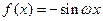 ,进一步要使
,进一步要使 处
处 取得最小值,则有
取得最小值,则有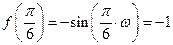
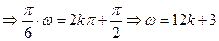 ,
,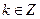 ;又
;又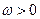 ,则有
,则有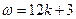 ,
,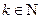 ;因此,由
;因此,由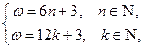 可得
可得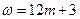 ,
,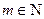 ;
;综上,使得函数
 满足“图像关于点
满足“图像关于点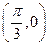 对称,且在
对称,且在 处
处 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当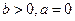 时,
时,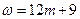 (
(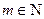 )或当
)或当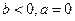 时,
时,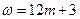 (
(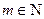 )”. ……………………………………………………14分
)”. ……………………………………………………14分(第III小题将根据学生对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分)

练习册系列答案
相关题目
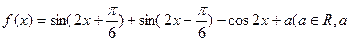 为常数).
为常数).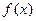 的最小正周期;(2)求函数
的最小正周期;(2)求函数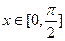 时,
时,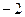 ,求
,求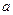 的值.
的值.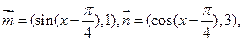
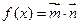 。
。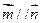 ,求
,求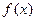 ;
;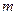 (
(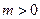 )个单位长度,再向下平移3个单位后图像对应的函数
)个单位长度,再向下平移3个单位后图像对应的函数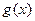 是奇函数,求
是奇函数,求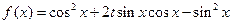 ,(1)当
,(1)当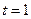 时,若
时,若 ,试求
,试求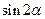 ;(2)若函数
;(2)若函数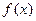 在区间
在区间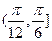 上是增函数,求实数
上是增函数,求实数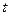 的取值范围.
的取值范围.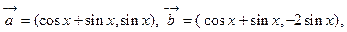
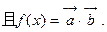
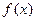 的解析式,并用
的解析式,并用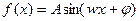 的形式表示(6分)
的形式表示(6分)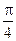 时,求此函数的最值及此时的x值.(6分)
时,求此函数的最值及此时的x值.(6分)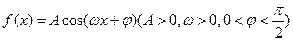 ,同时满足下列三个条件:
,同时满足下列三个条件: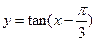 有相同的最小正周期;
有相同的最小正周期;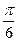 后关于y轴对称;
后关于y轴对称;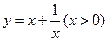 有相同的最小值。
有相同的最小值。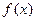 的解析式是 。
的解析式是 。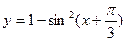 的最小正周期是 。
的最小正周期是 。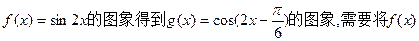 的图象( )
的图象( ) 个单位
个单位 个单位
个单位 .
.