摘要:(Ⅱ)证明:①若,则题意成立-------
网址:http://m.1010jiajiao.com/timu_id_497746[举报]
(本题满分14分)定义:对于函数![]() ,
,![]() .若
.若![]() 对定义域内的
对定义域内的![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为![]() 的
的![]() 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为![]() 的
的![]() 函数
函数![]() ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数![]() ,均有
,均有![]()
![]() ;
;
(3)对于值域![]() 的
的![]() 函数
函数![]() ,求证:
,求证:![]() .
.
(本题满分14分)定义:对于函数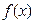 ,
,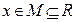 .若
.若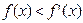 对定义域内的
对定义域内的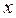 恒成立,则称函数
恒成立,则称函数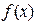 为
为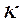 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为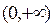 的
的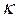 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为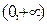 的
的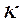 函数
函数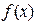 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数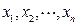 ,均有
,均有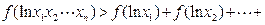
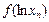 ;
;
(3)对于值域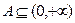 的
的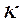 函数
函数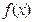 ,求证:
,求证: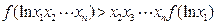 .
.
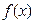 ,
,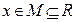 .若
.若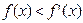 对定义域内的
对定义域内的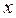 恒成立,则称函数
恒成立,则称函数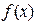 为
为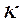 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为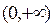 的
的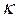 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为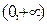 的
的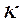 函数
函数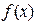 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数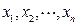 ,均有
,均有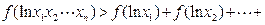
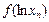 ;
;(3)对于值域
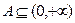 的
的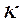 函数
函数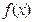 ,求证:
,求证: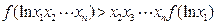 .
.选考题:从以下3题中选择2题做答,每题7分,若3题全做,则按前2题给分。
(1)(选修4—2 矩阵与变换)(本题满分7分)
变换![]() 是将平面上每个点
是将平面上每个点![]() 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点![]() 。
。
(Ⅰ)求变换![]() 的矩阵;
的矩阵;
(Ⅱ)圆![]() 在变换
在变换![]() 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)(选修4—4 参数方程与极坐标)(本题满分7分)
在极坐标系下,已知圆O:![]() 和直线
和直线![]() ,
,
(Ⅰ)求圆O和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
(3)(选修4—5 不等式证明选讲)(本题满分7分)
对于任意实数![]()
![]() 和
和![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
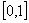 的函数同时满足以下三条:①对任意的
的函数同时满足以下三条:①对任意的
 ;②
;② ;③若
;③若
 则有
则有 成立.解答下列各题:
成立.解答下列各题: 的值;
的值; 在区间
在区间

 ,求证
,求证 .
.