摘要:所以 . ------4分
网址:http://m.1010jiajiao.com/timu_id_497497[举报]
以双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.设e1和e2分别为双曲线和它的共轭双曲线的离心率,给出下列结论:①e12+e22=e12e22②e12+e22≥4③e12+e22<e12e22④e12+e22>e12e22.其中正确结论的序号是
查看习题详情和答案>>
①②
①②
.(请写出所有正确结论的序号)以下四个关于圆锥曲线的命题中:
①双曲线
-
=1与椭圆
+
=1有相同的焦点;
②在平面内,设A、B为两个定点,P为动点,且|PA|+|PB|=k,其中常数k为正实数,则动点P的轨迹为椭圆;
③方程2x2-3x+1=0的两根可分别作为椭圆和双曲线的离心率;
④过双曲线x2-
=1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.
其中真命题的序号为
查看习题详情和答案>>
①双曲线
| x2 |
| 16 |
| y2 |
| 9 |
| x2 |
| 49 |
| y2 |
| 24 |
②在平面内,设A、B为两个定点,P为动点,且|PA|+|PB|=k,其中常数k为正实数,则动点P的轨迹为椭圆;
③方程2x2-3x+1=0的两根可分别作为椭圆和双曲线的离心率;
④过双曲线x2-
| y2 |
| 2 |
其中真命题的序号为
①④
①④
(写出所有真命题的序号).以下命题正确的有( )
(1)若a∥b,b∥c,则直线a,b,c共面;
(2)若a∥α,则a平行于平面α内的所有直线;
(3)若平面α内的无数条直线都与β平行,则α∥β;
(4)分别和两条异面直线都相交的两条直线必定异面.
(1)若a∥b,b∥c,则直线a,b,c共面;
(2)若a∥α,则a平行于平面α内的所有直线;
(3)若平面α内的无数条直线都与β平行,则α∥β;
(4)分别和两条异面直线都相交的两条直线必定异面.
查看习题详情和答案>>
以下五个命题中:
①若两直线平行,则两直线斜率相等;
②设F1、F2为两个定点,a为正常数,且||PF1|-|PF2||=2a,则动点P的轨迹为双曲线;
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④对任意实数k,直线l:kx-y+1-k=0与圆x2+y2-2y-4=0的位置关系是相交;
⑤P为椭圆
+
=1(a>b>0)上一点,F为它的一个焦点,则以PF为直径的圆与以长轴为直径的圆相切.
其中真命题的序号为
查看习题详情和答案>>
①若两直线平行,则两直线斜率相等;
②设F1、F2为两个定点,a为正常数,且||PF1|-|PF2||=2a,则动点P的轨迹为双曲线;
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④对任意实数k,直线l:kx-y+1-k=0与圆x2+y2-2y-4=0的位置关系是相交;
⑤P为椭圆
| x2 |
| a2 |
| y2 |
| b2 |
其中真命题的序号为
③④⑤
③④⑤
.(写出所有真命题的序号).本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(选修4—2 矩阵与变换)(本小题满分7分)
已知矩阵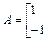
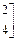 ,向量
,向量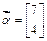 .
.
(Ⅰ) 求矩阵 的特征值
的特征值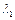 、
、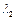 和特征向量
和特征向量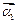 、
、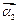 ;
;
(Ⅱ)求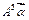 的值.
的值.
(2)(选修4—4 参数方程与极坐标)(本小题满分7分)
在极坐标系中,过曲线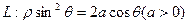 外的一点
外的一点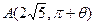 (其中
(其中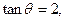
 为锐角)作平行于
为锐角)作平行于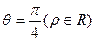 的直线
的直线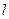 与曲线分别交于
与曲线分别交于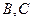 .
.
(Ⅰ) 写出曲线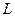 和直线
和直线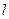 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为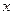 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若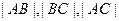 成等比数列,求
成等比数列,求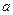 的值.
的值.
(3)(选修4—5 不等式证明选讲)(本小题满分7分)
已知正实数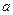 、
、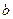 、
、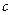 满足条件
满足条件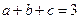 ,
,
(Ⅰ) 求证: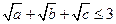 ;
;
(Ⅱ)若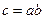 ,求
,求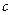 的最大值.
的最大值.