网址:http://m.1010jiajiao.com/timu_id_497308[举报]
1.(1)因为.files/image386.gif) ,所以
,所以.files/image388.gif)
又.files/image134.gif) 是圆O的直径,所以
是圆O的直径,所以.files/image391.gif)
又因为.files/image393.gif) (弦切角等于同弧所对圆周角)
(弦切角等于同弧所对圆周角)
所以.files/image395.gif) 所以
所以.files/image397.gif)
又因为.files/image399.gif) ,所以
,所以.files/image401.gif) 相似
相似
所以.files/image403.gif) ,即
,即.files/image158.gif)
(2)因为.files/image153.gif) ,所以
,所以.files/image406.gif) ,
,
因为.files/image151.gif) ,所以
,所以.files/image409.gif)
由(1)知:.files/image411.gif) 。所以
。所以.files/image413.gif)
所以.files/image415.gif) ,即圆的直径
,即圆的直径.files/image417.gif)
又因为.files/image419.gif) ,即
,即.files/image421.gif)
解得.files/image423.gif)
2.依题设有:.files/image425.gif)
令.files/image427.gif) ,则
,则.files/image429.gif)
.files/image431.gif)
.files/image429.gif)
.files/image433.gif)
.files/image435.gif)
.files/image435.gif)
.files/image438.gif)
3.将极坐标系内的问题转化为直角坐标系内的问题
点.files/image440.gif) 的直角坐标分别为
的直角坐标分别为.files/image442.gif)
故.files/image444.gif) 是以
是以.files/image140.gif) 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,
进而易知圆心为.files/image447.gif) ,半径为
,半径为.files/image449.gif) ,圆的直角坐标方程为
,圆的直角坐标方程为
.files/image451.gif) ,即
,即.files/image453.gif)
将.files/image455.gif) 代入上述方程,得
代入上述方程,得
.files/image457.gif) ,即
,即.files/image459.gif)
4.假设.files/image461.gif) ,因为
,因为.files/image463.gif) ,所以
,所以.files/image465.gif) 。
。
又由.files/image467.gif) ,则
,则.files/image469.gif) ,
,
所以.files/image471.gif) ,这与题设矛盾
,这与题设矛盾
又若.files/image473.gif) ,这与
,这与.files/image463.gif) 矛盾
矛盾
综上可知,必有.files/image475.gif) 成立
成立
同理可证.files/image477.gif) 也成立
也成立
命题成立
5. 解:由a1=S1,k=.files/image479.gif) .下面用数学归纳法进行证明.
.下面用数学归纳法进行证明.
1°.当n=1时,命题显然成立;
2°.假设当n=k(k.files/image481.gif) N*)时,命题成立,
N*)时,命题成立,
即1?2?3+2?3?4+……+ k(k+1)(k+2)=.files/image479.gif) k(k+1)(k+2)(k+3),
k(k+1)(k+2)(k+3),
则n=k+1时,1?2?3+2?3?4+……+ k(k+1)(k+2)+(k+1)(k+2)(k+3)=.files/image479.gif) k(k+1)(k+2)(k+3)+(k+1)(k+2)(k+3)
k(k+1)(k+2)(k+3)+(k+1)(k+2)(k+3)
=.files/image479.gif) ( k+1)(k+1+1)(k+1+2)(k+1+3)
( k+1)(k+1+1)(k+1+2)(k+1+3)
即命题对n=k+1.成立
由1°, 2°,命题对任意的正整数n成立.
6.(1)因为.files/image483.gif) ,
,.files/image485.gif) ,
,
.files/image487.gif) ,所以
,所以.files/image489.gif)
故事件A与B不独立。
(2)因为.files/image491.gif)
.files/image493.gif)
所以.files/image495.gif)
.files/image496.gif)
| 价格x | 9 | 905 | M | 10.5 | 11 |
| 销售量y | 11 | N | 8 | 6 | 5 |
 |
| y |
| x | 5 | 10 | 15 | 20 | 25 | 30 |
| y | 7.25 | 8.12 | 8.95 | 9.90 | 10.96 | 11.80 |
(2)求y与x的回归直线方程;
(3)预测所挂物体重量为27g时的弹簧长度(精确到0.01cm).
物体质量x:5 10 15 20 25 30
弹簧长度y:7.25 8.12 8.95 9.90 10.96 11.80
(1) 画出散点图;
(2)求Y对x的回归直线方程;
(3)预测所挂物体质量为
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
|
时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
|
10∶00 |
9.5 |
300 |
|
11∶00 |
9.6 |
220 |
注:油耗= ,可继续行驶距离=
,可继续行驶距离= ,
,
平均油耗 .
.
从上述信息可以推断在10∶00—11∶00这1小时内________ (填上所有正确判断的序号) .
向前行驶的里程为80公里;
向前行驶的里程不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
⑤ 平均车速超过80公里/小时.
查看习题详情和答案>>
(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
|
分组 |
频数累计 |
频数 |
频率 |
|
[10.75,10.85) |
6 |
6 |
0.06 |
|
[10.85,10.95) |
15 |
9 |
0.09 |
|
[10.95,11.05) |
30 |
15 |
0.15 |
|
[11.05,11.15) |
48 |
18 |
0.18 |
|
[11.15,11.25) |
▲ |
▲ |
▲ |
|
[11.25,11.35) |
84 |
12 |
0.12 |
|
[11.35,11.45) |
92 |
8 |
0.08 |
|
[11.45,11.55) |
98 |
6 |
0.06 |
|
[11.55,11.65) |
100 |
2 |
0.02 |
(Ⅰ)完成频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在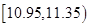 范围内的可能性是百分之几?
范围内的可能性是百分之几?
查看习题详情和答案>>