摘要：(2)若点P的坐标为(1,1),求证:直线PQ与圆相切,(3)试探究:当点P在圆O上运动时(不与A.B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明,若不是,请说明理由.
网址：http://m.1010jiajiao.com/timu_id_496934[举报]
（1）已知曲线C的极坐标方程为ρ2=
；
（Ⅰ）若以极点为原点，极轴所在的直线为x轴，求曲线C的直角坐标方程；
（Ⅱ）若P（x，y）是曲线C上的一个动点，求3x+4y的最大值
（2）已知a，b，c为实数，且a+b+c+2-2m=0，a2+
b2+
c2+m-1=0
（I）求证：a2+
b2+
c2≥
；
（II）求实数m的取值范围．
查看习题详情和答案>>
| 36 |
| 4cos2θ+9sin2θ |
（Ⅰ）若以极点为原点，极轴所在的直线为x轴，求曲线C的直角坐标方程；
（Ⅱ）若P（x，y）是曲线C上的一个动点，求3x+4y的最大值
（2）已知a，b，c为实数，且a+b+c+2-2m=0，a2+
| 1 |
| 4 |
| 1 |
| 9 |
（I）求证：a2+
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
（II）求实数m的取值范围．
（1）如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于D，DE⊥AC交AC延长线于点E，OE交AD于点F．（Ⅰ）求证：DE是⊙O的切线；
（Ⅱ）若
| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
（2）在直角坐标系中，以原点为极点，x轴的正半轴为极轴建坐标系，已知曲线
C：ρsin2θ=2acosθ（a＞0），已知过点P（-2，-4）的直线L的参数方程为：
|
（Ⅰ）写出曲线C和直线L的普通方程；
（Ⅱ）若|PM|，|MN|，|PN|成等比数列，求a的值．
直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
（Ⅰ）求
的取值范围；
（Ⅱ）过A、B两点分别作此抛物线的切线，两切线相交于N点.
求证：
；
（Ⅲ）若p是不为1的正整数，当
，△ABN的面积的取值范围为［5
，20］时，求该抛物线的方程.
直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
的取值范围；
；
，△ABN的面积的取值范围为［5
，20
外的任意一点，过点P的直线PA、PB分别与椭圆相切于A、B两点。
，求直线
的方程。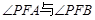
是否总是相等？若是，请给出证明。