题目内容
(1)已知曲线C的极坐标方程为ρ2=
;
(Ⅰ)若以极点为原点,极轴所在的直线为x轴,求曲线C的直角坐标方程;
(Ⅱ)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值
(2)已知a,b,c为实数,且a+b+c+2-2m=0,a2+
b2+
c2+m-1=0
(I)求证:a2+
b2+
c2≥
;
(II)求实数m的取值范围.
| 36 |
| 4cos2θ+9sin2θ |
(Ⅰ)若以极点为原点,极轴所在的直线为x轴,求曲线C的直角坐标方程;
(Ⅱ)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值
(2)已知a,b,c为实数,且a+b+c+2-2m=0,a2+
| 1 |
| 4 |
| 1 |
| 9 |
(I)求证:a2+
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
(II)求实数m的取值范围.
分析:(1)(I)根据的极坐标和直角坐标的互化公式,把曲线C的极坐标方程化为直角坐标方程,再化为参数方程.
(II)若P(x,y)是曲线C上的一个动点,则P(3cosθ,2sinθ),利用辅助角公式可得3x+4y=9cosθ+8sinθ=
sin(θ+∅),令sin(θ+∅)=1,求得3x+4y的最大值;
(2)(I)根据柯西不等式直接证明即可;
(II)将(I)中的a、b、c用等式a+b+c+2-2m=0,a2+
b2+
c2+m-1=0代入,消去a、b、c得到关于m的不等关系,解之即可求出m的范围.
(II)若P(x,y)是曲线C上的一个动点,则P(3cosθ,2sinθ),利用辅助角公式可得3x+4y=9cosθ+8sinθ=
| 145 |
(2)(I)根据柯西不等式直接证明即可;
(II)将(I)中的a、b、c用等式a+b+c+2-2m=0,a2+
| 1 |
| 4 |
| 1 |
| 9 |
解答:解:(1)(I)把曲线C的极坐标方程为ρ2=
;
化为直角坐标方程为
+
=1,
(II)若P(x,y)是曲线C上的一个动点,则P(3cosθ,2sinθ),
可得3x+4y=9cosθ+8sinθ=
sin(θ+∅),故当sin(θ+∅)=1时,3x+4y 取得最小值为
.
(2)(I)根据柯西不等式可得(a2+
b2+
c2)(1+22+32)≥(a×1+
×2+
×3)2=(a+b+c)2
∴a2+
b2+
c2≥
(II)∵a+b+c+2-2m=0,a2+
b2+
c2+m-1=0
∴1-m≥
解得:-
≤m≤1.
| 36 |
| 4cos2θ+9sin2θ |
化为直角坐标方程为
| x2 |
| 9 |
| y2 |
| 4 |
(II)若P(x,y)是曲线C上的一个动点,则P(3cosθ,2sinθ),
可得3x+4y=9cosθ+8sinθ=
| 145 |
| 145 |
(2)(I)根据柯西不等式可得(a2+
| 1 |
| 4 |
| 1 |
| 9 |
| b |
| 2 |
| c |
| 3 |
∴a2+
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c) 2 |
| 14 |
(II)∵a+b+c+2-2m=0,a2+
| 1 |
| 4 |
| 1 |
| 9 |
∴1-m≥
| (2m-2)2 |
| 14 |
解得:-
| 5 |
| 2 |
点评:本题主要考查点的极坐标和直角坐标的互化,辅助角公式的应用,以及不等式的证明等基础知识,是一道综合题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
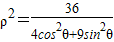 ;
;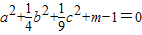
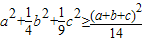 ;
;