网址:http://m.1010jiajiao.com/timu_id_496809[举报]
--数学.files/image102.jpg) 一、填空题:
一、填空题:
--数学.files/image102.jpg) 1、
1、--数学.files/image122.gif) 2、
2、--数学.files/image124.gif) 3、对任意
3、对任意--数学.files/image017.gif) 使
使--数学.files/image127.gif) 4、2 5、
4、2 5、--数学.files/image129.gif)
--数学.files/image102.jpg) 6、
6、--数学.files/image131.gif) 7、
7、--数学.files/image133.gif) 8、8
9、
8、8
9、--数学.files/image135.gif) 10、40
10、40
--数学.files/image102.jpg) 11、
11、--数学.files/image137.gif) 12、4
12、4
13、解:(1)解:--数学.files/image139.gif) ,
,
--数学.files/image102.jpg) 由
由--数学.files/image096.gif) ,有
,有--数学.files/image142.gif) ,
,
--数学.files/image102.jpg) 解得
解得--数学.files/image144.gif) 。
……7分
。
……7分
--数学.files/image102.jpg) (2)解法一:
(2)解法一:--数学.files/image146.gif) ……11分
……11分
--数学.files/image102.jpg)
--数学.files/image148.gif) 。 ……15分
。 ……15分
--数学.files/image102.jpg) 解法二:由(1),
解法二:由(1),--数学.files/image144.gif) ,得
,得--数学.files/image151.gif)
--数学.files/image102.jpg) ∴
∴--数学.files/image153.gif)
--数学.files/image155.gif)
--数学.files/image102.jpg) ∴
∴--数学.files/image157.gif) ……10分
……10分
--数学.files/image102.jpg) 于是
于是--数学.files/image159.gif) ,
,
--数学.files/image102.jpg)
--数学.files/image161.gif) ……12分
……12分
--数学.files/image102.jpg) 代入得
代入得--数学.files/image163.gif) 。
……15分
。
……15分
14、(1)解:①若直线--数学.files/image106.gif) 的斜率不存在,即直线是
的斜率不存在,即直线是--数学.files/image166.gif) ,符合题意。 ……2分
,符合题意。 ……2分
--数学.files/image168.jpg)
--数学.files/image102.jpg) ②若直线
②若直线--数学.files/image106.gif) 斜率存在,设直线
斜率存在,设直线--数学.files/image106.gif) 为
为--数学.files/image172.gif) ,即
,即--数学.files/image174.gif) 。
。
--数学.files/image102.jpg) 由题意知,圆心
由题意知,圆心--数学.files/image176.gif) 以已知直线
以已知直线--数学.files/image106.gif) 的距离等于半径2,即:
的距离等于半径2,即:--数学.files/image179.gif) ,
,
--数学.files/image102.jpg) 解之得
解之得--数学.files/image181.gif) ……5分
……5分
--数学.files/image102.jpg) 所求直线方程是
所求直线方程是--数学.files/image166.gif) ,
,--数学.files/image184.gif) ……6分
……6分
--数学.files/image102.jpg) (2)解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为
(2)解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为--数学.files/image174.gif)
--数学.files/image102.jpg) 由
由--数学.files/image187.gif) 得
得--数学.files/image189.gif) ……8分
……8分
--数学.files/image102.jpg) 又直线
又直线--数学.files/image191.gif) 与
与--数学.files/image106.gif) 垂直,由
垂直,由--数学.files/image194.gif) 得
得--数学.files/image196.gif) ……11分
……11分
--数学.files/image102.jpg) ∴
∴--数学.files/image198.gif)
--数学.files/image102.jpg) ……13分
……13分
--数学.files/image200.gif) 为定值。
为定值。
故--数学.files/image202.gif) 是定值,且为6。
……15分
是定值,且为6。
……15分
已知动圆 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 的轨迹为曲线
的轨迹为曲线 ;设
;设 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 于
于 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
已知动圆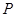 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心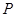 的轨迹为曲线
的轨迹为曲线 ;设
;设 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 于
于 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记 的面积为
的面积为 ,
, 的面积为
的面积为 ,令
,令 ,求
,求 的最大值.
的最大值.
 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 的轨迹为曲线
的轨迹为曲线 ;设
;设 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 于
于 两个不同的点.
两个不同的点.(1)求曲线
 的方程;
的方程;(2)试探究
 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;(3)记
 的面积为
的面积为 ,
, 的面积为
的面积为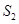 ,令
,令 ,求
,求 的最大值.
的最大值.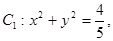 直线
直线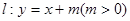 与圆
与圆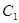 相切,且交椭圆
相切,且交椭圆 于
于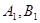 两点,
两点,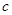 是椭圆的半焦距,
是椭圆的半焦距,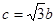 ,
,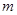 的值;
的值;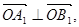 求椭圆
求椭圆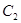 的方程;
的方程; ,直线AS,BS与直线
,直线AS,BS与直线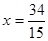 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.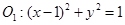 外切,与圆
外切,与圆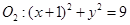 内切.
内切.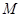 的轨迹
的轨迹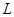 的方程;
的方程;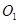 的直线
的直线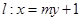 与轨迹
与轨迹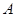 、
、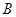 两点,请问
两点,请问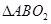 (
(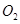 为圆
为圆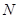 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线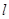 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.