题目内容
已知圆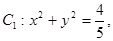 直线
直线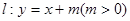 与圆
与圆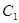 相切,且交椭圆
相切,且交椭圆 于
于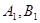 两点,
两点,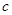 是椭圆的半焦距,
是椭圆的半焦距,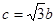 ,
,
(Ⅰ)求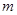 的值;
的值;
(Ⅱ)O为坐标原点,若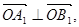 求椭圆
求椭圆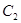 的方程;
的方程;
(Ⅲ) 在(Ⅱ)的条件下,设椭圆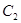 的左右顶点分别为A,B,动点
的左右顶点分别为A,B,动点 ,直线AS,BS与直线
,直线AS,BS与直线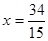 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.
(Ⅰ)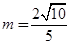 ;(Ⅱ)椭圆
;(Ⅱ)椭圆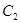 的方程为
的方程为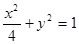 ;(Ⅲ)
;(Ⅲ)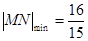 .
.
【解析】
试题分析:(Ⅰ)直线与圆相切,则圆心到直线的距离等于半径.设圆的圆心为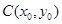 半径分别为
半径分别为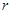 ,直线的方程为
,直线的方程为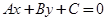 .若直线与圆相切,则圆心到直线的距离
.若直线与圆相切,则圆心到直线的距离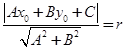 ,将已知条件代入这个公式,即可得
,将已知条件代入这个公式,即可得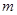 的值.
的值.
(Ⅱ)将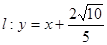 代入得:
代入得: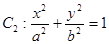 得关于
得关于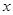 的二次方程.设
的二次方程.设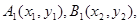 则
则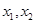 是这个方程的两个根.因为,所以
是这个方程的两个根.因为,所以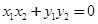 ,再结合韦达定理,可得一个含
,再结合韦达定理,可得一个含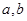 的等式,与
的等式,与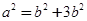 联立解方程组即可求得
联立解方程组即可求得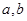 的值.
的值.
(Ⅲ)思路一、在(Ⅱ)的条件下,椭圆的方程为: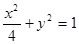 ,动点
,动点 ,则将其代入椭圆方程,便得:
,则将其代入椭圆方程,便得: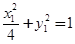 ①.设
①.设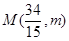 ,
,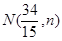 ,则
,则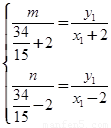 .两式相乘再利用①式可消去
.两式相乘再利用①式可消去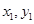 得
得 ,再用重要不等式便可得线段MN的长度的最小值.
,再用重要不等式便可得线段MN的长度的最小值.
思路二、选定一个量作为变量,其余的量都用这个量来表示,最终用这个量表示出线段MN的长度.
那么选哪 一个量作为变量呢?显然直线AS的斜率存在,设为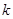 且
且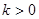 ,然后用
,然后用 表示出点
表示出点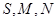 的坐标,从而表示出线段MN的长度. 再用重要不等式便可得线段MN的长度的最小值.
的坐标,从而表示出线段MN的长度. 再用重要不等式便可得线段MN的长度的最小值.
试题解析:(Ⅰ)直线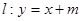 与圆
与圆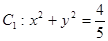 相切,所以
相切,所以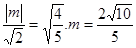 4分
4分
(Ⅱ) 将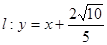 代入得:
代入得:
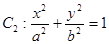 得:
得:
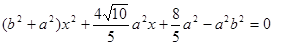 ①
①
设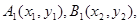 则
则
 ②
②
因为
由已知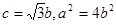 代人②
代人②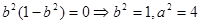
所以椭圆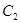 的方程为
的方程为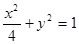 8分
8分
(Ⅲ)法一、在(Ⅱ)的条件下,椭圆的方程为: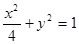 ,将动点
,将动点 的坐标代入椭圆方程,便得:
的坐标代入椭圆方程,便得: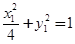 ①
①
设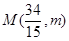 ,
,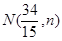 ,则
,则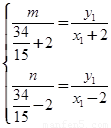 .两式相乘得
.两式相乘得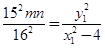 ②
②
由①得: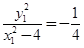 ,代入②得:
,代入②得: ,显然
,显然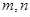 异号.
异号.
所以线段MN的长度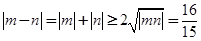 ,当
,当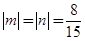 时取等号.
时取等号.
法二、显然直线AS的斜率存在,设为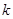 且
且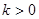 则
则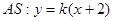
依题意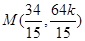 ,由
,由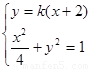 得:
得: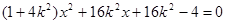
设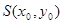 则
则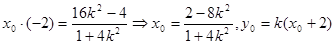 即
即
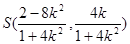 ,又B(2,0)所以
,又B(2,0)所以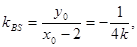 BS:
BS: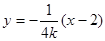
由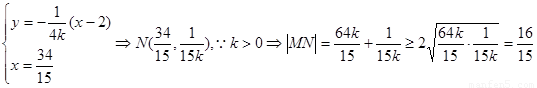
所以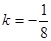 时:
时: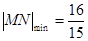 12分
12分
考点:1、椭圆的方程;2、直线与圆锥曲线;3、函数的最值.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
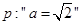 ,
,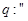 直线
直线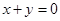 与圆
与圆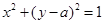 相切
相切 ,则
,则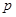 是
是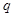 的
的 ,定直线l的方程为
,定直线l的方程为 .动圆C与圆C1外切,且与直线l相切.
.动圆C与圆C1外切,且与直线l相切. 为轨迹M与直线PQ围成的封闭图形的面积,求
为轨迹M与直线PQ围成的封闭图形的面积,求