摘要:又∵EO 面AEC.BD1∥面AEC ∴BD1∥平面AEC (2)连结B1D1.AB1 ∵DD1 ∥=BB1 ∴B1D1 ∥=BD ∴∠AD1B1即为BD与AD1所成的角 在正方体中有面对角线AD1 = D1B1 = AB1 ∴△AD1B1为正三角形 ∴∠AD1B1 = 60° 即异面直线BD与AD1所成的角的大小为60°
网址:http://m.1010jiajiao.com/timu_id_494614[举报]
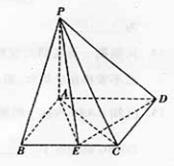
(本题满分14分)如图,点P在正方形ABCD所在的平面外,PD⊥面ABCD,∠PAD=45°,空间一点E在平面ABCD上的射影是点B,且PB⊥面AEC.
(1)求直线AD与平面AEC所成的角的正切值;
(2)若F是AP的中点,求直线BF与CE所成角.
查看习题详情和答案>>
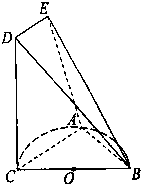 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tanθ=
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tanθ=| 3 | 4 |
(1)证明:面ABE⊥面ACDE;
(2)求四棱锥B-ACDE的体积.
 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.(1)证明:CD⊥SD;
(2)证明:CM∥面SAD;
(3)求四棱锥S-ABCD的体积.
 (2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=
(2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF= 中,底面
中,底面 是平行四边形,
是平行四边形, ,且
,且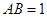 ,
,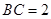 ,又
,又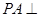 底面
底面 ,又
,又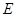 为边
为边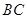 上异于
上异于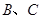 的点,且
的点,且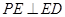 .
. 到平面
到平面 的距离.
的距离.